题目内容
如图,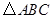 是
是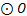 的内接三角形,
的内接三角形,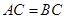 ,
, 为
为 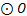 中
中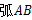 上一点,延长
上一点,延长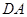 至点
至点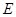 ,使
,使 .
.
(1)求证: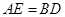 ;
;
(2)若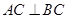 ,求证:
,求证: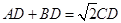 .
.
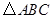 是
是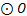 的内接三角形,
的内接三角形,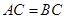 ,
, 为
为 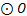 中
中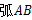 上一点,延长
上一点,延长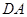 至点
至点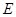 ,使
,使 .
.
(1)求证:
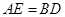 ;
;(2)若
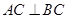 ,求证:
,求证: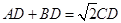 .
.证明见解析.
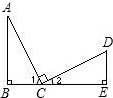
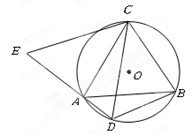
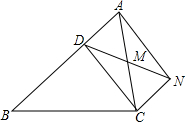
试题分析:(1)根据同弧上的圆周角相等,得∠CBA=∠CDE,则∠ACB=∠ECD,可证明△ACE≌△BCD,则AE=BD;
(2)根据已知条件得,∠CED=∠CDE=45°,则DE=
 CD,从而证出结论.
CD,从而证出结论.试题解析:(1)在△ABC中,∠CAB=∠CBA.
在△ECD中,∠E=∠CDE.
∵∠CBA=∠CDE,(同弧上的圆周角相等),
∴∠E=∠CDE=∠CAB=∠CBA,
∵∠E+∠ECD+∠EDC=180°,∠CAB+∠ACB+∠ABC=180°,
∴∠ACB=∠ECD,
∴∠ACB﹣∠ACD=∠ECD﹣∠ACD.
∴∠ACE=∠BCD,
在△ACE和△BCD中,∠ACE=∠BCD;CE=CD;AC=BC,
∴△ACE≌△BCD.
∴AE=BD;
(2)若AC⊥BC,∵∠ACB=∠ECD.
∴∠ECD=90°,
∴∠CED=∠CDE=45°,
∴DE=
 CD,
CD,又∵AD+BD=AD+EA=ED,
∴AD+BD=
 CD.
CD.
练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
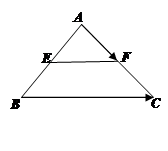
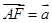 ,
, .
.
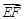 、
、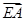 (用向量
(用向量 、
、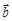 表示);
表示);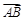 、
、 方向上的分向量.
方向上的分向量.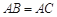 ,
,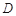 是
是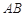 上一点,
上一点,  于点
于点 ,
,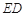 的延长线交
的延长线交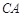 的延长线于点
的延长线于点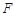 .求证:
.求证: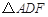 是等腰三角形.
是等腰三角形.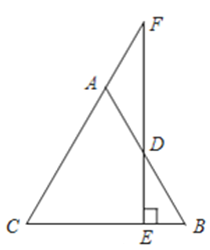
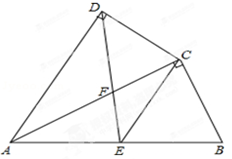
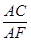 的值.
的值.