题目内容
【题目】在平面直角坐标系xOy中，直线
与双曲线
的一个交点为P（2，m），与x轴、y轴分别交于点A，B．
（1）求m的值；
（2）若PA=2AB，求k的值．
【答案】（1）m=4（2）k=1或3
【解析】（1）将点P的坐标代入反比例函数的解析式即可求得m的值；
（2）作
轴于点C，根据点P(2,4)在y=kx+b上，得b=42k，直线y=kx+b(k≠0)与x轴、y轴分别交于点A，B，写出A
，B
，分两种情况进行讨论即可.
（1）∵函数
的图像经过
，
∴
，
解得：
；
(2)点P(2,4)在y=kx+b上，
∴4=2k+b，
∴b=42k，
∵直线y=kx+b(k≠0)与x轴、y轴分别交于点A，B，
∴A，B，
如图，点A在x轴负半轴，点B在y轴正半轴时，
∵PA=2AB，
∴AB=PB，则OA=OC，
∴
，解得k=1；
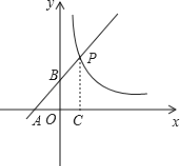
当点A在x轴正半轴,点B在y轴负半轴时,
，解得，k=3.
∴k=1或k=3.
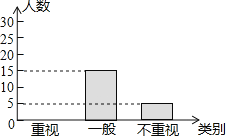
【题目】某教研机构为了了解初中生课外阅读名著的现状，随机抽取了某校50名初中生进行调查，依据相关数据绘制成了以下不完整的统计图，请根据图中信息解答下列问题：
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
（1）求表格中a，b的值；
（2）请补全统计图；
（3）若某校共有初中生2000名，请估计该校“重视课外阅读名著”的初中生人数．
【题目】某公司生产的某种产品每件成本为40元，经市场调查整理出如下信息：
①该产品90天售量(n件)与时间(第x天)满足一次函数关系，部分数据如下表：
时间（第x天） | 1 | 2 | 3 | 10 | … |
日销售量（n件） | 198 | 196 | 194 | ? | … |
②该产品90天内每天的销售价格与时间（第x天）的关系如下表：
时间（第x天） | 1≤x＜50 | 50≤x≤90 |
销售价格（元/件） | x+60 | 100 |
(1)求出第10天日销售量；
(2)设销售该产品每天利润为y元，请写出y关于x的函数表达式，并求出在90天内该产品的销售利润最大?最大利润是多少?（提示：每天销售利润=日销售量×（每件销售价格－每件成本)）
(3)在该产品销售的过程中，共有多少天销售利润不低于5400元，请直接写出结果.
