题目内容
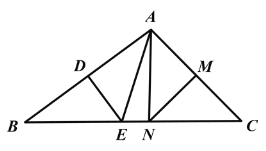
【题目】如图,在△ABC中,∠A=30°,∠B=90°,BC=6, 一个边长为2的正方形DEFH沿边CA方向向下平移,平移开始时点F与点C重合,当正方形DEFH的平移距离为__________时,有DC2=AE2+BC2成立,

【答案】![]()
【解析】
连接CD,设平移的距离为x,则CF=x,根据勾股定理得到CD2=22+(x+2)2,由∠A=30°,∠B=90°,BC=6,得到AC=12,AE=12-2-x=10-x,再根据DC2=AE2+BC2列出方程即可求解.
连接CD,设平移的距离为x,则CF=x,
根据勾股定理得到CD2=22+(x+2)2,
∵∠A=30°,∠B=90°,BC=6,
∴AC=12,AE=12-2-x=10-x,
∴AE2+BC2=(10-x)2+62,
∵DC2=AE2+BC2
∴22+(x+2)2=(10-x)2+62,
解得x=![]()
故填![]() .
.


练习册系列答案
相关题目