Question

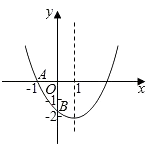
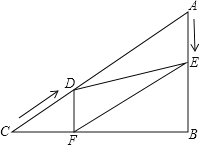
【题目】两个反比例函数y= （k＞1）和y= 在第一象限内的图象如图所示，点P在y= 的图象上，PC⊥x轴于点C，交y= 的图象于点A，PD⊥y轴于点D，交y= 的图象于点B，BE⊥x轴于点E，当点P在y= 图象上运动时，以下结论：①BA与DC始终平行；②PA与PB始终相等；③四边形PAOB的面积不会发生变化；④△OBA的面积等于四边形ACEB的面积．其中一定正确的是（填序号）

Answer 1

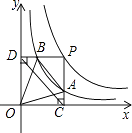
【答案】①③④
【解析】解：设点P的坐标为（m， ），则点A（m， ），点C（m，0），点B（ ， ），点D（0， ）， ∴PB=m﹣ = ，PD=m，PA= ﹣ = ，PD=m，PC= ，
∵ = ， = = ，
∴BA∥DC，①成立；
∵PB= ，PA= ，
∴当m2=k时，PA=PB，②不成立；
S矩形OCPD=k，S△OBD= ，S△OAC= ，
S四边形PAOB=S矩形OCPD﹣S△OBD﹣S△OBD=k﹣1，
∵k为固定值，
∴③成立；
S梯形BECA= （AC+BE）EC= （ + ）（m﹣ ）= ，S△OBA=S四边形PAOB﹣S△PAB=k﹣1﹣ （m﹣ ）（ ﹣ ）= ，
∴S梯形BECA=S△OBA ， ④成立．
综上可知：一定正确的为①③④．
故答案为：①③④．
设出点P的坐标，由此可得出A、C、B、D点的坐标，由点的坐标即可表示出各线段的长度，根据线段间的比例关系即可得出BA∥DC，即①成立；找出当PA=PB时，m的值，由此发现②不一定成立；③根据反比例函数系数k的几何意义可得出三角形OBD、OAC以及矩形OCPD的面积，分割图形即可得出S四边形PAOB=k﹣1，即③成立；根据各边长度计算出S梯形BECA ， 结合三角形的面积公式求出S△OBA ， 发现二者相等，由此得知④成立．综上即可得出结论．