题目内容
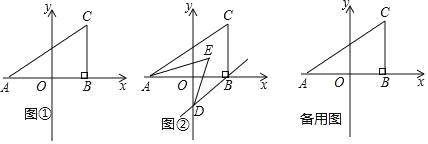
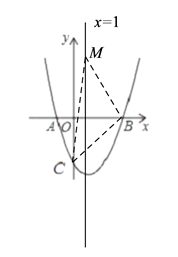
【题目】如图，已知抛物线y=x2+bx+c经过A（-1，0）、B（3，0）两点，点C是抛物线与y轴的交点．
（1）求抛物线的解析式和顶点坐标；
（2）当0＜x＜3时，求y的取值范围；
（3）在抛物线的对称轴上是否存在点M，使△BCM是等腰三角形，若存在请直接写出点M坐标，若不存在请说明理由．
【答案】
（1）解：把A（﹣1，0）、B（3，0）分别代入y=x2+bx+c中，
得： 
，解得： 
，
∴抛物线的解析式为y=x2﹣2x﹣3．
∵y=x2﹣2x﹣3=（x﹣1）2﹣4，
∴抛物线顶点坐标为（1，﹣4）
（2）解：∵在y=x2﹣2x﹣3中，当 
时， 
；当 
时， 
；抛物线顶点坐标为（1，-4），
∴当0＜x＜3时， 
的取值范围为：﹣4≤y＜0
（3）解：存在.由（1）和（2）可知，抛物线的对称轴为直线 
，点C的坐标为（0，-3），
∴可设点M的坐标为（1，m），由此可得：CB2=18；CM2= 
；BM2= 
.
①当CB2=CM2时，有 
，解得： 
；
②当CB2=BM2时，有 
，解得： 
；
③当CM2=BM2时，有 
，解得： 
；
综上所述，存在点M使△BCM是等腰三角形，M的坐标为： 
、 
、 
、 
、 
.
【解析】（1）方法一、将点A、B的坐标分别代入函数解析式，建立方程组，求出b、c的值，就可求出函数解析式；再求出顶点坐标即可。方法二、根据已知点的坐标特点，设函数解析式为交点式，即可求出函数解析式。
（2）由抛物线的开口方向和顶点坐标，可知当x=1时，y最小值=4，当x=3时，y=0；当x=0时，y=3 ，由此可求出当0＜x＜3时，求y的取值范围。
（3）利用函数解析式求出点C的坐标，根据已知可知点M在抛物线的对称轴上，因此设点M的坐标为（1，m），再根据点B、C的坐标，分别表示出CB2、CM2、BM2。然后分情况讨论：①当CB2=CM2时，②当CB2=BM2时，③当CM2=BM
