题目内容
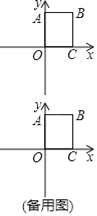
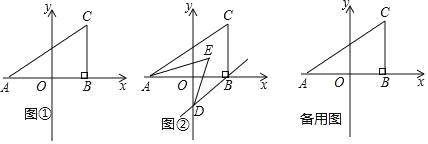
【题目】如图①,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+![]() =0,过C作CB⊥x轴于B.
=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积;
(2)如图②,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等?若存在,求出P点的坐标;若不存在,请说明理由.
【答案】(1)4;(2)∠AED=45°;(3)P(0,-1)或(0,3).
【解析】
(1)先依据非负数的性质可求得a、b的值,从而可得到点A、点B和点C的坐标,接下来,依据三角形的面积公式求解即可;
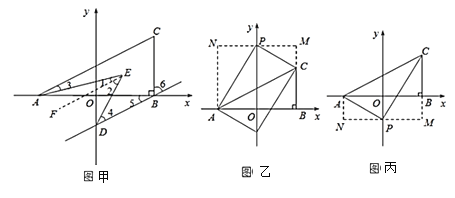
(2)如图甲所示:过E作EF∥AC.首先依据平行线的性质可知∠ODB=∠6,∠CAB=∠5,接下来,依据平行公理的推理可得到BD∥AC∥EF,然后,依据平行线的性质可得到∠1=∠3,∠2=∠4,然后,依据角平分线的性质可得到∠3=![]() ∠CAB,∠4=
∠CAB,∠4=![]() ∠ODB,最后,依据∠AED=∠1+∠2=∠3+∠4求解即可;
∠ODB,最后,依据∠AED=∠1+∠2=∠3+∠4求解即可;
(3)①当P在y轴正半轴上时,设点P(0,t),分别过点P,A,B作MN∥x轴,AN∥y轴,BM∥y轴,交于点M,N,然后,用含t的式子表示出AN,CM的长,然后依据S三角形ACP=S梯形MNAC-S三角形ANP-S三角形CMP列出关于t的方程求解即可;②当P在y轴负半轴上时,如图丙分别过点P,A,B作MN∥x轴,AN∥y轴,BM∥y轴,交于点M,N,设点P(0,t),然后用含t的式子表示出AN、CM的长,最后,依据S三角形ACP=S梯形MNAC-S三角形ANP-S三角形CMP列方程求解即可.
解:(1)∵(a+2)2+![]() =0,
=0,
∴a+2=0,b-2=0,
∴a=-2,b=2,
∵CB⊥AB,
∴A(-2,0),B(2,0),C(2,2),
∴△ABC的面积=![]() ×2×4=4;
×2×4=4;
(2)∵CB//y轴,BD//AC,
∴∠CAB=∠5,∠ODB=∠6,∠CAB+∠ODB=∠5+∠6=90°,
过E作EF//AC,如图①
∵BD//AC,
∴BD//AC//EF,
∵AE、DE分别平分∠CAB、∠ODB,
∴∠3=![]() ∠CAB=∠1,∠4=
∠CAB=∠1,∠4=![]() ∠ODB=∠2,
∠ODB=∠2,
∴∠AED=∠1+∠2=![]() (∠CAB+∠ODB)=45°
(∠CAB+∠ODB)=45°
(3)①当P在y轴正半轴上时,如图②,
设P(0,t),过P作MN//x轴,AN//y轴,BM//y轴,
∵S△APC=S梯形MNAC-S△CMP-S△ANP=4,
∴![]() -t-(t-2)=4,
-t-(t-2)=4,
解得:t=3,
②当P在y轴负半轴上时,如图③,设P(0,t),过P作MN//x轴,AN//y轴,BM//y轴,
∵S△APC=S梯形MNAC-S△ANP-S△CMP=4,
∴![]() +t-(2-t)=4,
+t-(2-t)=4,
解得:t= -1,
∴P(0,-1)或(0,3).
故答案为(1)4;(2)∠AED=45°;(3)P(0,-1)或(0,3).

 名校课堂系列答案
名校课堂系列答案