题目内容
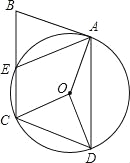
【题目】有一个直径为1m的圆形铁皮，要从中剪出一个最大的圆心角为90°的扇形ABC，如图所示．
（1）求被剪掉阴影部分的面积：
（2）用所留的扇形铁皮围成一个圆锥，该圆锥的底面圆的半径是多少？
【答案】（1）
平方米；（2）
米；
【解析】
试题（1）先根据圆周角定理可得弦BC为直径，即可得到AB=AC，根据特殊角的锐角三角函数值可求得AB的长，最后根据扇形的面积公式即可求得结果；
（2）设圆锥底面圆的半径为r，而弧BC的长即为圆锥底面的周长，根据弧长公式及圆的周长公式即可求得结果.
（1）∵∠BAC=90°
∴弦BC为直径
∴AB=AC
∴AB=AC=BC·sin45°=
∴S阴影=S⊙O-S扇形ABC=
(
)2-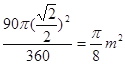
；
（2）设圆锥底面圆的半径为r，而弧BC的长即为圆锥底面的周长，由题意得
2r=
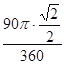，解得r=
答：（1）被剪掉的阴影部分的面积为
；（2）该圆锥的底面圆半径是.
练习册系列答案
阅读快车系列答案
相关题目
