题目内容
【题目】平面直角坐标系![]() 中,点
中,点![]() 、
、![]() 分别在函数
分别在函数![]() 与
与![]() 的图象上,
的图象上, ![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() 、
、![]() 。
。

(1)若![]() 轴,求
轴,求![]() 的面积;
的面积;
(2)若![]() 是以
是以![]() 为底边的等腰三角形,且a
为底边的等腰三角形,且a![]() ,求
,求![]() 的值;
的值;
(3)作边长为2的正方形![]() ,使
,使![]() 轴,点
轴,点![]() 在点
在点![]() 的左上方,那么,对大于或等于的任意实数
的左上方,那么,对大于或等于的任意实数![]() ,
, ![]() 边与函数
边与函数![]() 的图象都有交点,请说明理由。
的图象都有交点,请说明理由。
【答案】(1) ![]() 的面积为3;
的面积为3;
(2) ![]() 的值为-3;
的值为-3;
(3)理由见解析.
【解析】试题分析:(1)根据反比例函数系数k的几何意义得出△OAC与△OBC的面积,再求和即可;
(2)分别用a、b表示出A、B两点的坐标,再根据勾股定理得出OA2=a2+(![]() )2,OB2=b2+(-
)2,OB2=b2+(-![]() )2,由OA=OB即可得出结论;
)2,由OA=OB即可得出结论;
(3)根据题意画出图形,设直线CD与函数y=![]() (x>0)的图象交点为F,用a表示出A、C两点的坐标,进而可得出F点的坐标,求出FC的最大值,进而可得出结论.
(x>0)的图象交点为F,用a表示出A、C两点的坐标,进而可得出F点的坐标,求出FC的最大值,进而可得出结论.
试题解析:(1)如图1,AB交y轴于C,
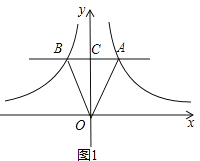
∵AB∥x轴,
∴S△OAC=![]() ×|3|=
×|3|=![]() ,S△OBC=
,S△OBC=![]() ×|-3|=
×|-3|=![]() ,
,
∴S△OAB=S△OAC+S△OBC=3;
(2)∵点A、B分别在函数y=![]() (x>0)与y=-
(x>0)与y=-![]() (x<0)的图象上,A、B的横坐标分别为a、b.
(x<0)的图象上,A、B的横坐标分别为a、b.
∴A(a, ![]() )、B(b,
)、B(b, ![]() ),
),
∴OA2=a2+(![]() )2,OB2=b2+(-
)2,OB2=b2+(-![]() )2,
)2,
当OA=OB时,OA2=OB2
∴a2+(![]() )2=b2+(-
)2=b2+(-![]() )2,
)2,
整理得:a2b2(a2-b2)=9(a2-b2).
∵a+b≠0,a>0,b<0,
∴a2-b2≠0
∴a2b2=9,
∴ab=-3;
(3)设直线CD与函数y=![]() (x>0)的图象交点为F,如图2,
(x>0)的图象交点为F,如图2,
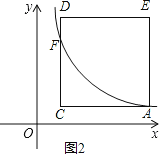
∵A点坐标为(a, ![]() ),正方形ACDE的边长为3,
),正方形ACDE的边长为3,
∴C点坐标为(a-3, ![]() ),
),
∴F点的坐标为(a-3, ![]() ),
),
∴FC=![]() -
-![]() =
=![]() .
.
∵a(a-3)=(a-![]() )2-
)2-![]() ,当a>
,当a>![]() 时,a(a-3)的值随a的值的增大而增大,
时,a(a-3)的值随a的值的增大而增大,
∴a(a-3)的最小值为3,
∴FC的最大值为3,即FC≤DC,
∴CD与函数y=![]() (x>0)的图象有交点.
(x>0)的图象有交点.
特别地,当a=3时,点A的坐标为(3,1),此时C(1,1)、D(1,3),
此时点D落在函数y=![]() (x>0)的图象上.
(x>0)的图象上.
∴点F在线段DC上,即对大于或等于3的任意实数a,CD边与函数y=![]() (x>0)的图象都有交点.
(x>0)的图象都有交点.

 阅读快车系列答案
阅读快车系列答案
