题目内容
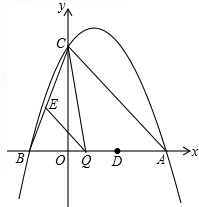 已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,3),与x轴交于点A、B,点A的坐标为(3,0),点O为坐标原点.
已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,3),与x轴交于点A、B,点A的坐标为(3,0),点O为坐标原点.(1)求该抛物线的解析式;
(2)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得OF+DF最小?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标.
考点:二次函数综合题
专题:综合题
分析:(1)将点A、C的坐标代入可得出a、c的值,继而确定抛物线解析式;
(2)作O′使O′与O关于直线AC对称,连接O'D,O'D交AC于F,过点F且平行于x的直线l与抛物线交于点P,点P为所求;
(3)设Q(m,0),且-1≤m≤3,由QE∥AC,可得△BEQ∽△BCA,利用对应边成比例可得出EH的长,由S=S△BQC-S△BEQ,可得S关于m的表达式,利用配方法求最值即可.
(2)作O′使O′与O关于直线AC对称,连接O'D,O'D交AC于F,过点F且平行于x的直线l与抛物线交于点P,点P为所求;
(3)设Q(m,0),且-1≤m≤3,由QE∥AC,可得△BEQ∽△BCA,利用对应边成比例可得出EH的长,由S=S△BQC-S△BEQ,可得S关于m的表达式,利用配方法求最值即可.
解答:解:(1)将点A(3,0),点C(0,3)代入抛物线解析式:
,
解得:
,
故抛物线解析式:y=-x2+2x+3.
(2)存在.
如图所示:
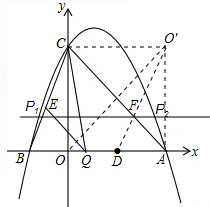
作O′使O′与O关于直线AC对称,连接O'D,O'D交AC于F,过点F且平行于x的直线l与抛物线交于点P,点P为所求.
易求O′(3,3),设直线O′D的解析式:y=k1x+b,
则可得:
,
解得:
,
故直线O'D的解析式为:y=3x-6
设直线AC解析式:y=k2x+3,
将点A(3,0)代入可得:0=3k2+3,
解得:k2=-1,
故直线AC的解析式为:y=-x+3,
由
得:
,即F(
,
),
∴直线l:y=
,
由
得:
,
,
即P(1+
,
)或(1-
,
).
(3)设Q(m,0),且-1≤m≤3,
作EH⊥x轴于H,
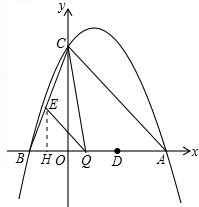
∵QE∥AC,
∴△BEQ∽△BCA,
∴
=
,
即
=
,EH=
(m+1),
∴S=S△BQC-S△BEQ=
(m+1)×3-
(m+1)×
(m+1)=
(m-1)2+
,
∵-1≤m≤3,
∴当m=1时,△CAE面积最大,此时Q(1,0).
|
解得:
|
故抛物线解析式:y=-x2+2x+3.
(2)存在.
如图所示:

作O′使O′与O关于直线AC对称,连接O'D,O'D交AC于F,过点F且平行于x的直线l与抛物线交于点P,点P为所求.
易求O′(3,3),设直线O′D的解析式:y=k1x+b,
则可得:
|
解得:
|
故直线O'D的解析式为:y=3x-6
设直线AC解析式:y=k2x+3,
将点A(3,0)代入可得:0=3k2+3,
解得:k2=-1,
故直线AC的解析式为:y=-x+3,
由
|
|
| 9 |
| 4 |
| 3 |
| 4 |
∴直线l:y=
| 3 |
| 4 |
由
|
|
|
即P(1+
| ||
| 2 |
| 3 |
| 4 |
| ||
| 2 |
| 3 |
| 4 |
(3)设Q(m,0),且-1≤m≤3,
作EH⊥x轴于H,

∵QE∥AC,
∴△BEQ∽△BCA,
∴
| EH |
| OC |
| BO |
| BA |
即
| mEH |
| 3 |
| m+1 |
| 4 |
| 3 |
| 4 |
∴S=S△BQC-S△BEQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| 2 |
∵-1≤m≤3,
∴当m=1时,△CAE面积最大,此时Q(1,0).
点评:本题考查了二次函数的综合,涉及了待定系数法求函数解析式、轴对称求最短路径及配方法求二次函数最值,解答综合性题目,关键还是基础知识的掌握,注意数形结合思想的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
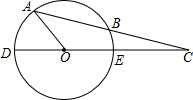 如图,DE为⊙O的直径,AB为⊙O的弦,延长AB与直线DE交于C,且BC等于圆的半径,已知∠AOD=54°,则∠ACD=( )
如图,DE为⊙O的直径,AB为⊙O的弦,延长AB与直线DE交于C,且BC等于圆的半径,已知∠AOD=54°,则∠ACD=( )| A、18° | B、22.5° |
| C、30° | D、15° |
若直角三角形的两条直角边各扩大一倍,则斜边( )
| A、不变 | B、扩大一倍 |
| C、扩大两倍 | D、扩大四倍 |
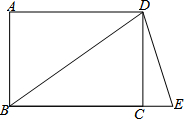 如图,矩形ABCD中,点E在BC的延长线上,BD为对角线,且BD=BE,∠ADB=40°,则∠E的度数是( )
如图,矩形ABCD中,点E在BC的延长线上,BD为对角线,且BD=BE,∠ADB=40°,则∠E的度数是( )| A、60° | B、70° |
| C、75° | D、80° |
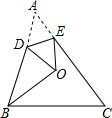 如图,△ABC中,O为三边垂直平分线的交点,将△ABC沿DE折叠,使顶点A恰好落在O点处,若BD=OB,则∠C的度数为( )
如图,△ABC中,O为三边垂直平分线的交点,将△ABC沿DE折叠,使顶点A恰好落在O点处,若BD=OB,则∠C的度数为( )| A、45° | B、54° |
| C、60° | D、72 |
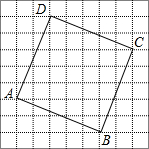 如图,在9×9网格中,每个小正方形的边长均为1,正方形ABCD的顶点都在网格的格点上.
如图,在9×9网格中,每个小正方形的边长均为1,正方形ABCD的顶点都在网格的格点上.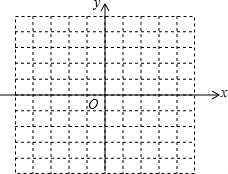 已知四边形ABCD四个点的坐标分别为A(-5,-3)、B(-2,3)、C(0,1)、D(1,-4).
已知四边形ABCD四个点的坐标分别为A(-5,-3)、B(-2,3)、C(0,1)、D(1,-4).