题目内容
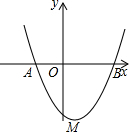如图，抛物线y=x2-2x-3与x轴分别交于A，B两点．（1）求A，B两点的坐标；
（2）求抛物线顶点M关于x轴对称的点M′的坐标，并判断四边形AMBM′是何特殊平行四边形．（不要求说明理由）
分析：（1）求抛物线与x轴的交点，令y=0，求x即可；
（2）根据对称性来判断，可知线段AB与线段MM'互相垂直平分，根据菱形的判定定理进行判断．
（2）根据对称性来判断，可知线段AB与线段MM'互相垂直平分，根据菱形的判定定理进行判断．
解答：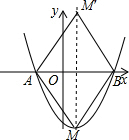
解：（1）由y=0得x2-2x-3=0．
解得x1=-1，x2=3．
∴点A的坐标（-1，0），点B的坐标（3，0）．
（2）∵-
=1，
=-4，
∴M（1，-4），
∵点M与点M'关于x轴对称，
∴M'（1，4）．由此可知四边形AMBM'的对角线互相垂直平分，
∴四边形AMBM'是菱形．
解：（1）由y=0得x2-2x-3=0．解得x1=-1，x2=3．
∴点A的坐标（-1，0），点B的坐标（3，0）．
（2）∵-
| b |
| 2a |
| 4ac-b2 |
| 4a |
∴M（1，-4），
∵点M与点M'关于x轴对称，
∴M'（1，4）．由此可知四边形AMBM'的对角线互相垂直平分，
∴四边形AMBM'是菱形．
点评：本题考查了抛物线解析式的运用，利用对称性判断菱形的方法．
练习册系列答案
黄冈小状元同步计算天天练系列答案
相关题目
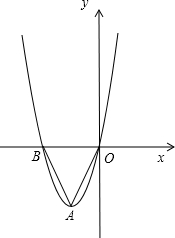如图，抛物线y=x2+4x与x轴分别相交于点B、O，它的顶点为A，连接AB，AO．
16、如图，抛物线y=-x2+2x+m（m＜0）与x轴相交于点A（x1，0）、B（x2，0），点A在点B的左侧．当x=x2-2时，y
已知如图，抛物线y=x2+（k2+1）x+k+1的对称轴是直线x=-1，且顶点在x轴上方．设M是直线x=-1左侧抛物线上的一动点，过点M作x轴的垂线MG，垂足为G，过点M作直线x=-1的垂线MN，垂足为N，直线x=-1与x轴的交于H点，若M点的横坐标为x，矩形MNHG的周长为l．
（2013•扬州）如图，抛物线y=x2-2x-8交y轴于点A，交x轴正半轴于点B．