Question

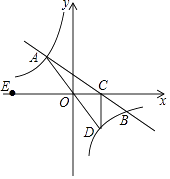
【题目】如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与反比例函数y= （m≠0）的图象交于二、四象限内的A、B两点，与x轴交于C点，点B的坐标为（12，n）
， OA=10，E为x轴负半轴上一点，且tan∠AOE= ．

（1）求该反比例函数和一次函数的解析式；
（2）延长AO交双曲线于点D，连接CD，求△ACD的面积．

Answer 1

【答案】
（1）解：如图，过A作AF⊥x轴于F，

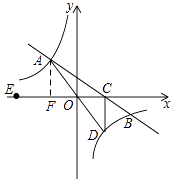
∵OA=10，tan∠AOE= ，

∴可设AF=4a，OF=3a，则由勾股定理可得：

（3a）2+（4a）2=102，

解得a=2，

∴AF=8，OF=6，

∴A（﹣6，8），

代入反比例函数y= ，可得m=﹣48，

∴反比例函数解析式为：y=﹣ ，

把点B（12，n）代入y=﹣ ，可得n=﹣4，

∴B（12，﹣4），

设一次函数的解析式为y=kx+b，则

，

解得 ，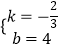

∴一次函数的解析式为y=﹣ x+4；

（2）解：在一次函数y=﹣ x+4中，令y=0，则x=6，即C（6，0），

∵A（﹣6，8）与点D关于原点成中心对称，

∴D（6，﹣8），

∴CD⊥x轴，

∴S△ACD=S△ACO+S△CDO

= CO×AF+ CO×CD

= ×6×8+ ×6×8

=48．

【解析】(1)过A作AF⊥x轴于F，根据锐角三角函数的定义，及勾股定理得出AF=8，OF=6，进而得出A点的坐标，用待定系数法求出反比例函数的解析式，进而求出B点的坐标，再利用待定系数法求出一次函数的解析式；
（2）求出C点的坐标，根据A与点D关于原点成中心对称求出D点的坐标，然后利用S△ACD=S△ACO+S△CDO列式计算即可。