题目内容
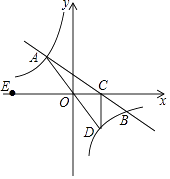
【题目】已知菱形ABCD的对角线相交于O,点E,F分别在边AB、BC上,且BE=BF,射线EO,FO分别交边CD、AD于G,H.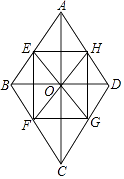
(1)求证:四边形EFGH为矩形;
(2)若OA=4,OB=3,求EG的最小值.
【答案】
(1)证明:∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AB∥CD,AD∥BC,
∴∠BAO=∠DCO,∠AOE=∠GOC,
∴△AOE≌△COG(ASA),
∴OE=OG,
同理得:OH=OF,
∴四边形EFGH是平行四边形,
∵BE=BF,∠ABD=∠CBD,OB=OB,
∴△EBO≌△FBO,
∴OE=OF,
∴EG=FH,
∴四边形EFGH是矩形;
(2)解:∵垂线段最短,
∴当OE⊥AB时,OE最小,
∵OA=4,OB=3,∠AOB=90°,
∴AB2=OA2+OB2=25,
∴AB=5,
∴ ![]() OA×OB=
OA×OB= ![]() AB×OE,
AB×OE,
3×4=5×OE,
OE= ![]() ,
,
∵OE=OG,
∴EG= ![]() .
.
答:EG的最小值是 ![]() .
.
【解析】(1)利用菱形的性质可证得四边形EFGH的对角线互相平分,证出它是平行四边形,再证出其对角线相等,得出它是矩形;(2)求EG的最小值也就是OE 的最小值,根据垂线段最短,可知当OEOE⊥AB时,OE最小,进而EGz最小.
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

练习册系列答案
相关题目