题目内容
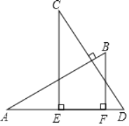
【题目】如图,将矩形ABCD绕点C旋转得到矩形FECG,点E在AD上,延长ED交FG于点H. 
(1)求证:△EDC≌△HFE;
(2)连接BE、CH.四边形BEHC是怎样的特殊四边形?证明你的结论.
(3)连接BE、CH.当AB与BC的比值为时,四边形BEHC为菱形.
【答案】
(1)证明:∵矩形FECG由矩形ABCD旋转得到,
∴FE=AB=DC,∠F=∠EDC=90°,FH∥EC,
∴∠FHE=∠CED.
在△EDC和△HFE中, 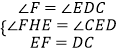 ,
,
∴△EDC≌△HFE.
(2)证明:①四边形BEHC为平行四边形,
∵△EDC≌△HFE,
∴EH=EC.
∵矩形FECG由矩形ABCD旋转得到,
∴EH=EC=BC,EH∥BC,
∴四边形BEHC为平行四边形.
(3)![]()
【解析】(3)解:连接BE. 
∵四边形BEHC为菱形,
∴BE=BC.
由旋转的性质可知BC=EC.
∴BE=EC=BC.
∴△EBC为等边三角形.
∴∠EBC=60°.
∴∠ABE=30°.
∴AB:BE= ![]() :2.
:2.
又∵BE=CB,
∴AB与BC的比值= ![]() .
.
故答案为: ![]() .
.
(1)依据题意可得到FE=AB=DC,∠F=∠EDC=90°,FH∥EC,利用平行线的性质可证明∠FHE=∠CED,然后依据AAS证明△EDC≌△HFE即可;(2)由全等三角形的性质可知EH=EC,由旋转的性质可得到BC=EC,从而可证明EH=BC,最后依据平行四边形的判定定理进行证明即可;(3)连接BE.可证明△EBC为等边三角形,则∠ABE=30°,利用特殊锐角三角函数值可得到AB:BE= ![]() :2.
:2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目