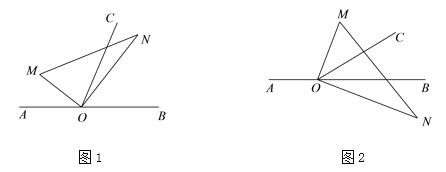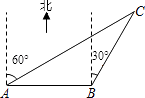题目内容
【题目】建立模型：
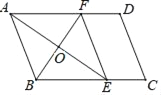
如图1，已知△ABC，AC=BC，∠C=90°，顶点C在直线l上．
操作：
过点A作AD⊥l于点D，过点B作BE⊥l于点E．求证：△CAD≌△BCE．
模型应用：
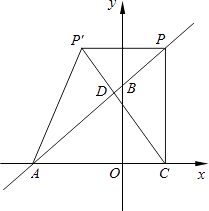
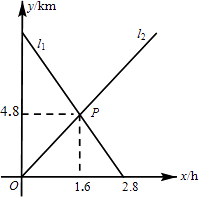
（1）如图2，在直角坐标系中，直线l1：y=
x+4与y轴交于点A，与x轴交于点B，将直线l1绕着点A顺时针旋转45°得到l2．求l2的函数表达式．
（2）如图3，在直角坐标系中，点B（8，6），作BA⊥y轴于点A，作BC⊥x轴于点C，P是线段BC上的一个动点，点Q（a，2a﹣6）位于第一象限内．问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形，若能，请求出此时a的值，若不能，请说明理由．
【答案】（1）y=
x+4；（2）a的值为
或4．
【解析】
试题分析：操作：根据余角的性质，可得∠ACD=∠CBE，根据全等三角形的判定，可得答案；
应用（1）根据自变量与函数值的对应关系，可得A、B点坐标，根据全等三角形的判定与性质，可得CD，BD的长，根据待定系数法，可得AC的解析式；
（2）根据全等三角形的性质，可得关于a的方程，根据解方程，可得答案．
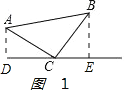
解：操作：如图1：
，
∵∠ACD+∠BCE=90°，∠BCE+∠CBE=90°，
∴∠ACD=∠CBE．
在△ACD和△CBE中，
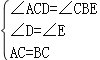
∴△CAD≌△BCE（AAS）；
（1）∵直线y=
x+4与y轴交于点A，与x轴交于点B，
∴A（0，4）、B（﹣3，0）．
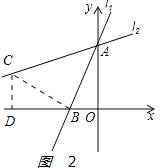
如图2：
，
过点B做BC⊥AB交直线l2于点C，过点C作CD⊥x轴
在△BDC和△AOB中，
，
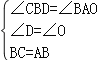△BDC≌△AOB（AAS），
∴CD=BO=3，BD=AO=4．OD=OB+BD=3+4=7，
∴C点坐标为（﹣7，3）．
设l2的解析式为y=kx+b，将A，C点坐标代入，得
，
解得
l2的函数表达式为y=x+4；
（2）由题意可知，点Q是直线y=2x﹣6上一点．
如图3：
，
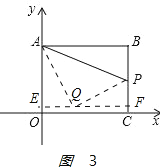过点Q作EF⊥y轴，分别交y轴和直线BC于点E、F．
在△AQE和△QPF中，
，
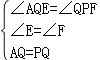∴△AQE≌△QPF（AAS），
AE=QF，即6﹣（2a﹣6）=8﹣a，
解得a=4
如图4：
，
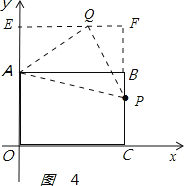过点Q作EF⊥y轴，分别交y轴和直线BC于点E、F，
AE=2a﹣12，FQ=8﹣a．
在△AQE和△QPF中，
，
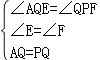△AQE≌△QPF（AAS），
AE=QF，即2a﹣12=8﹣a，
解得a=
；
综上所述：A、P、Q可以构成以点Q为直角顶点的等腰直角三角形，a的值为或4．
