题目内容
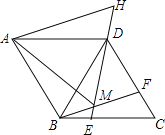
【题目】已知等边△ABC，点D和点B关于直线AC轴对称．点M（不同于点A和点C）在射线CA上，线段DM的垂直平分线交直线BC的于N，
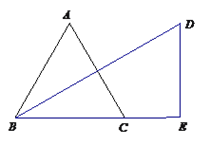
（1）如图，过点D作DE⊥BC，交BC的延长线于E，若CE＝5，求BC的长；
（2）如图，若点M在线段AC上，求证：△DMN为等边三角形；
（3）连接CD，BM，若
，直接写出
．
【答案】（1）10；（2）∠DCA=60°（3）
或1
【解析】试题分析：（1）连接CD，构造含30°角的直角三角形DCE，根据BC=DC进行计算即可；
（2）过点N作NG⊥CD于G，作NH⊥AC于H，得到∠H=∠DGN=90°，先判定Rt△MNH≌Rt△DNG（HL），得到∠CMQ=∠NDQ，进而得出∠2=∠5=60°，最后结合NM=ND，判定△DMN为等边三角形即可；
（3）需要分两种情况进行讨论：当点M在线段AC上时，连接AD，BD；当点M在CA延长线上时，连接AD，分别根据等高三角形的面积之比等于底边之比进行计算即可．
试题解析：解：（1）如图1，连接CD，∵△ABC是等边三角形，点D和点B关于直线AC轴对称，∴BC=DC，∠ACB=∠ACD=60°，∴∠DCE=60°．∵DE⊥CE，CE=5，∴∠CDE=30°，∴CD=2CE=10，∴BC=10；
（2）如图2，过点N作NG⊥CD于G，作NH⊥AC于H，则∠H=∠DGN=90°．∵△ABC是等边三角形，点D和点B关于直线AC轴对称，∴∠1=∠2=60°，∴∠3=60°=∠4，即NC平分∠GCH，∴NG=NH．∵线段DM的垂直平分线交直线BC于点N，∴NM=ND．在Rt△MNH和Rt△DNG中，∵NM=ND，NG=NH，∴Rt△MNH≌Rt△DNG（HL），∴∠CMQ=∠NDQ．又∵∠MQC=∠DQN，∴∠2=∠5=60°．∵NM=ND，∴△DMN为等边三角形；
（3）①如图3，当点M在线段AC上时，连接AD，BD，则BD⊥AC，BP=DP．∵△ACD和△MND都是等边三角形，∴AD=CD，∠ADM=∠CDN，MD=ND，∴△ADM≌△CDN，∴AM=CN．∵ 
=3，∴
，∴
，∴
，即
，∴
，∴
；
②如图4，当点M在CA延长线上时，连接AD，同理可得，△ADM≌△CDN，∴AM=CN．∵ 
=3，∴
，∴
，即
，∴BN=CN，∴
=1．
综上所述， 
=
或1．
