题目内容
已知:二次函数y=x2+bx+c(b、c为常数).(1)若二次函数的图象经过A(-2,-3)和B(2,5)两点,求此二次函数的解析式;
(2)若(1)中的二次函数的图象过点P(m+1,n2+4n),且m≠n,求m+n的值.
分析:(1)由于二次函数的图象经过A、B两点,可将它们的坐标代入二次函数的解析式中,即可求得待定系数的值;
(2)已知抛物线的图象经过P点,可将其坐标代入(1)得出的解析式中,即可求得m+n的值.
(2)已知抛物线的图象经过P点,可将其坐标代入(1)得出的解析式中,即可求得m+n的值.
解答:解:(1)把A(-2,-3)和B(2,5)两点代入y=x2+bx+c得
,
解得
∴所求二次函数的解析式为y=x2+2x-3;
(2)∵二次函数图象过点P(m+l,n2+4n)
∴n2+4n=(m+l)2+2(m+l)-3
n2+4n=m2+4m
(n-m)(n+m+4)=0
∵m≠n,∴n+m+4=0
即m+n=-4.
|
解得
|
∴所求二次函数的解析式为y=x2+2x-3;
(2)∵二次函数图象过点P(m+l,n2+4n)
∴n2+4n=(m+l)2+2(m+l)-3
n2+4n=m2+4m
(n-m)(n+m+4)=0
∵m≠n,∴n+m+4=0
即m+n=-4.
点评:本题考查了用待定系数法求函数解析式的方法,同时还考查了方程(组)的解等知识,难度不大.

练习册系列答案
相关题目
 已知:二次函数的表达式为y=2x2+4x-1.
已知:二次函数的表达式为y=2x2+4x-1.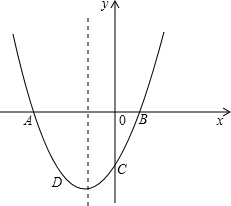 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.