题目内容
 已知:二次函数的表达式为y=2x2+4x-1.
已知:二次函数的表达式为y=2x2+4x-1.(1)设这个函数图象的顶点坐标为P,与y轴的交点为A,求P、A两点的坐标;
(2)将二次函数的图象向上平移1个单位,设平移后的图象与x轴的交点为B、C(其中点B在点C的左侧),求B、C两点的坐标及tan∠APB的值.
分析:(1)利用配方法将原函数解析式变为y=2(x+1)2-3,则可求得这个函数图象的顶点坐标P,又由x=0时,y=-1,求得点A的坐标;
(2)首先求得平移后的二次函数的解析式,则可求得B、C的坐标,然后求得AB,AP,PB的长,则可得∠PAB=90°,则问题得解.
(2)首先求得平移后的二次函数的解析式,则可求得B、C的坐标,然后求得AB,AP,PB的长,则可得∠PAB=90°,则问题得解.
解答: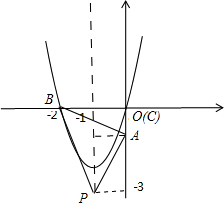 解:(1)y=2x2+4x-1=2(x2+2x)-1=2(x+1)2-3,
解:(1)y=2x2+4x-1=2(x2+2x)-1=2(x+1)2-3,
∴顶点P的坐标为:P(-1,-3),
当x=0时,y=-1,
∴与y轴的交点坐标为:A(0,-1);
(2)平移后的解析式为:y=2x2+4x.
令y=0,得2x2+4x=0,
∴x1=0,x2=-2.
∴平移后的图象与x轴的交点坐标为:B(-2,0),C(0,0);
由A(0,-1),B(-2,0),P(-1,-3),
可得:AB=
=
,AP=
=
,PB=
=
.
∴AB2+AP2=PB2.
∴∠PAB=90°.
∴tan∠APB=
=
=1.
 解:(1)y=2x2+4x-1=2(x2+2x)-1=2(x+1)2-3,
解:(1)y=2x2+4x-1=2(x2+2x)-1=2(x+1)2-3,∴顶点P的坐标为:P(-1,-3),
当x=0时,y=-1,
∴与y轴的交点坐标为:A(0,-1);
(2)平移后的解析式为:y=2x2+4x.
令y=0,得2x2+4x=0,
∴x1=0,x2=-2.
∴平移后的图象与x轴的交点坐标为:B(-2,0),C(0,0);
由A(0,-1),B(-2,0),P(-1,-3),
可得:AB=
| 22+12 |
| 5 |
| 22+12 |
| 5 |
| 12+32 |
| 10 |
∴AB2+AP2=PB2.
∴∠PAB=90°.
∴tan∠APB=
| AB |
| PA |
| ||
|
点评:此题考查了二次函数一般式与顶点式的转化,勾股定理的应用以及二次函数与一元二次方程的关系等知识.此题难度适中,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 ,纵坐标增大
,纵坐标增大 ,纵坐标增大
,纵坐标增大 分别作为点A的横、纵坐标;把顶点的横坐标增加
分别作为点A的横、纵坐标;把顶点的横坐标增加 ,纵坐标增加
,纵坐标增加 分别作为点B的横、纵坐标,则A,B两点也在抛物线y=ax2+2x+3(a≠0)上。
分别作为点B的横、纵坐标,则A,B两点也在抛物线y=ax2+2x+3(a≠0)上。 ,纵坐标增大
,纵坐标增大 分别作为点A的横、纵坐标;把顶点的横坐标增加
分别作为点A的横、纵坐标;把顶点的横坐标增加 ,纵坐标增加
,纵坐标增加 分别作为点B的横、纵坐标,则A,B两点也在抛物线y=ax2+2x+3(a≠0)上.
分别作为点B的横、纵坐标,则A,B两点也在抛物线y=ax2+2x+3(a≠0)上.