题目内容
已知:二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,其中点A的坐标是(-2,0),点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OC<OB)是方程x2-10x+24=0的两个根.(1)求B、C两点的坐标;
(2)求这个二次函数的解析式.
分析:(1)解方程求已知方程的两根,根据题意确定B、C两点坐标;
(2)抛物线过A(-2,0),B(6,0),设交点式,把C(0,4)代入求待定系数即可.
(2)抛物线过A(-2,0),B(6,0),设交点式,把C(0,4)代入求待定系数即可.
解答:解:(1)解方程x2-10x+24=0,得x1=6,x2=4,
∵OC<OB,
∴B(6,0),C(0,4);
(2)∵抛物线与x轴交于A(-2,0),B(6,0)
设抛物线解析式y=a(x+2)(x-6)
把C(0,4)代入解析式,得
4=a(0+2)(0-6),解得a=-
,
y=-
(x+2)(x-6)
即y=-
x2+
x+4.
∵OC<OB,
∴B(6,0),C(0,4);
(2)∵抛物线与x轴交于A(-2,0),B(6,0)
设抛物线解析式y=a(x+2)(x-6)
把C(0,4)代入解析式,得
4=a(0+2)(0-6),解得a=-
| 1 |
| 3 |
y=-
| 1 |
| 3 |
即y=-
| 1 |
| 3 |
| 4 |
| 3 |
点评:本题考查了解一元二次方程,点的坐标的求法,待定系数法求二次函数解析式的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:二次函数的表达式为y=2x2+4x-1.
已知:二次函数的表达式为y=2x2+4x-1.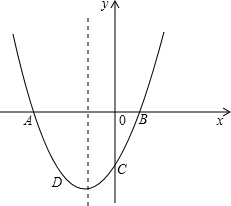 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.