题目内容
【题目】如图,正方形BCPQ对角线交于点A,将一块等腰直角三角形中45°角的顶点放在A点,斜边AG所在的直线交BC于点D,直角边AH所在的直角交BC于点E. 
(1)在边BC上取一点M,连接AM,AD平分∠BAM,求证:AE平分∠MAC;
(2)在(1)的条件下,请判断BD、CE、DE之间的数量关系,并证明你的结论.
【答案】
(1)证明:∵∠DAE=45°,
∴∠DAM+∠EAM=45°,
在正方形BCPQ中,BP⊥CQ,∴∠BAC=90°,
∴∠BAD+∠CAE=45°,
∴∠DAM+∠EAM=∠BAD+∠EAC
AD平分∠BAM,
∴∠BAD=∠DAM
∴∠EAM=∠EAC 即AE平分∠MAC.
(2)解:结论:BD2+CE2=DE2.
证明:延长AM到点F,使AF=AB,
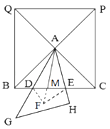
在正方形BCPQ中,AB=AC,∠BAC=90°,
∴AF=AC,∠ABC=∠ACB=45°,
∵∠BAD=∠DAM 由(1)知,∠EAM=∠EAC,
又AF=AF,
∴△FAD≌△BAD,△FAE≌△CAE,
∴∠AFD=∠ABC=45°,DF=BD,∠AFE=∠ACB=45°,EF=EC,
∴∠DFE=90°,
在Rt△DEF中,DF2+EF2=DE2,
∴BD2+CE2=DE2.
【解析】(1)只要证明∠DAM+∠EAM=∠BAD+∠EAC,由AD平分∠BAM,可得∠BAD=∠DAM即可推出∠EAM=∠EAC.
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°),还要掌握正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形)的相关知识才是答题的关键.

 黄冈创优卷系列答案
黄冈创优卷系列答案
