题目内容
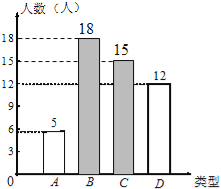
【题目】每年11月的最后一个星期四是感恩节,小龙调查了初三年级部分同学在感恩节当天将以何种方式表达感谢帮助过自己的人.他将调查结果分为如下四类:A类﹣﹣当面致谢;B类﹣﹣打电话;C类﹣﹣发短信息或微信;D类﹣﹣写书信.他将调查结果绘制成如图不完整的扇形统计图和条形统计图:

请你根据图中提供的信息完成下列各题:
(1)补全条形统计图;
(2)在A类的同学中,有3人来自同一班级,其中有1人学过主持.现准备从他们3人中随机抽出两位同学主持感恩节主题班会课,请你用树状图或表格求出抽出的两人都没有学过主持的概率.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)观察统计图,先用A类的人数除以它所占的百分比得到总人数,再利用扇形统计图计算出C类人数,接着计算出D类人数,然后补全条形统计图;
(2)通过列表法展示所有12种等可能情况,再找出1人主持过班会而另一人没主持过班会的结果数,然后根据概率公式求解.
解:(1)调查的学生总数为5÷10%=50(人),
C类人数为50×![]() =15(人),
=15(人),
D类人数为50﹣5﹣15﹣12=18(人),
条形统计图为:
(2)设主持过班会的两人分别为A1、A2,另两人分别为B1、B2,填表如下:
结果 第二人
第一人 A1A2B1B2
A1(A1,A2) (A1,B1) (A1,B2)
A2(A2,A1) (A2,B1) (A2,B2)
B1(B1,A1) (B1,A2) (B1,B2)
B2(B2,A1) (B2,A2) (B2,B1)
由列表可知,共有12种等可能情况,其中有8种符合题意,
所以P(抽出1人主持过班会而另一人没主持过班会)=![]() .
.

练习册系列答案
相关题目