题目内容
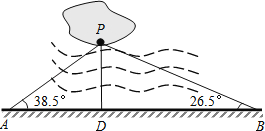
【题目】如图,益阳市梓山湖中有一孤立小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,小张在小道上测得如下数据:AB=80.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小张求出小桥PD的长并确定小桥在小道上的位置.(以A,B为参照点,结果精确到0.1米)
(参考数据:sin38.5°=0.62,cos38.5°=0.78,tan38.5°=0.80,sin26.5°=0.45,cos26.5°=0.89,tan26.5°=0.50)
【答案】小桥PD的长度约为24.6米,位于AB之间距B点约49.2米.
【解析】
试题分析:设PD=x米,在Rt△PAD中表示出AD,在Rt△PDB中表示出BD,再由AB=80.0米,可得出方程,解出即可得出PD的长度,继而也可确定小桥在小道上的位置.
解:设PD=x米,
∵PD⊥AB,
∴∠ADP=∠BDP=90°,
在Rt△PAD中,tan∠PAD=![]() ,
,
∴AD=![]() ≈
≈![]() =
=![]() x,
x,
在Rt△PBD中,tan∠PBD=![]() ,
,
∴DB=![]() ≈
≈![]() =2x,
=2x,
又∵AB=80.0米,
∴![]() x+2x=80.0,
x+2x=80.0,
解得:x≈24.6,即PD≈24.6(米),
∴DB=49.2(米).
答:小桥PD的长度约为24.6米,位于AB之间距B点约49.2米.

练习册系列答案
相关题目