题目内容
 已知:如图,梯形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.
已知:如图,梯形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.
(1)求证:四边形ABFC是平行四边形;
(2)若BC⊥AB,且BC=12,AB=8,求AF的长.
(1)证明:∵E为BC的中点,
∴BE=CE,
∵AB∥CD,
∴∠BAE=∠CFE,∠ABE=∠FCE,
在△ABE和△FCE中, ,
,
∴△ABE≌△FCE(AAS),
∴AE=FE,
又∵在四边形ABFC中,BE=CE,
∴四边形ABFC是平行四边形;
(2)解:∵BC=12,E是BC的中点,
∴BE= BC=
BC= ×12=6,
×12=6,
∵BC⊥AB,
∴AE= =
= =10,
=10,
∴AF=2AE=2×10=20.
分析:(1)根据中点的定义可得BE=CE,再根据两直线平行,内错角相等可得∠BAE=∠CFE,∠ABE=∠FCE,然后利用“角角边”证明△ABE和△FCE全等,根据全等三角形对应边相等可得AE=FE,然后根据对角线互相平分的四边形是平行四边形证明;
(2)先求出BE的长,再利用勾股定理列式求出AE,然后根据平行四边形的对角线互相平分可得AF=2AE,代入数据计算即可得解.
点评:本题考查了梯形的性质,全等三角形的判定与性质,平行四边形的判定与性质,综合题,但难度不大,熟练掌握各判定与性质是解题的关键.
∴BE=CE,
∵AB∥CD,
∴∠BAE=∠CFE,∠ABE=∠FCE,
在△ABE和△FCE中,
 ,
,∴△ABE≌△FCE(AAS),
∴AE=FE,
又∵在四边形ABFC中,BE=CE,
∴四边形ABFC是平行四边形;
(2)解:∵BC=12,E是BC的中点,
∴BE=
 BC=
BC= ×12=6,
×12=6,∵BC⊥AB,
∴AE=
 =
= =10,
=10,∴AF=2AE=2×10=20.
分析:(1)根据中点的定义可得BE=CE,再根据两直线平行,内错角相等可得∠BAE=∠CFE,∠ABE=∠FCE,然后利用“角角边”证明△ABE和△FCE全等,根据全等三角形对应边相等可得AE=FE,然后根据对角线互相平分的四边形是平行四边形证明;
(2)先求出BE的长,再利用勾股定理列式求出AE,然后根据平行四边形的对角线互相平分可得AF=2AE,代入数据计算即可得解.
点评:本题考查了梯形的性质,全等三角形的判定与性质,平行四边形的判定与性质,综合题,但难度不大,熟练掌握各判定与性质是解题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )
9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )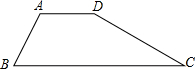 已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=
已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=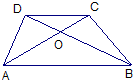 8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB=
8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB= 已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.
已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.