题目内容
【题目】在平面直角坐标系中,点O是坐标原点,点A的坐标是(-a,a),点B的坐标是(c,b),满足 ![]() .
.
(1)a为不等式2x+6<0的最大整数解,求a的值并判断点A在第几象限;
(2)在(1)的条件下,求△AOB的面积;
(3)在(2)的条件下,若两个动点M(k-1,k),N(-2h+10,h),请你探索是否存在以两个动点M、N为端点的线段MN//AB,且MN=AB,若存在,求M、N两点的坐标;若不存在,请说明理由.
【答案】
(1)
解:不等式2x+6<0的解为x<-3,x的最大整数解为-2即a=-2;
则A(2,-2),在第四象限。
(2)
解:将a=2代入题中的方程组可得 ![]() 解得
解得 ![]()
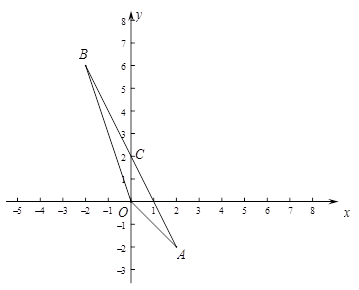
则B(-2,6),如图,在坐标系在描出A(2,-2)和B(-2,6),
连接OB,OA,AB交y轴于C,观察图象可得C(2,0),
则 ![]() 。
。
(3)
解:由(1)、(2)可得A(2,-2),B(-2,6),
因为AB//MN,且AB=MN,
所以可以看作由AB平移到MN,
由平移的性质可得
![]() 或
或 ![]()
解得  或
或 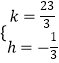
故M( ![]() ,
, ![]() ),N(
),N( ![]() ,
, ![]() )或M(
)或M( ![]() ,
, ![]() ),N(
),N( ![]() ,
, ![]() )。
)。
【解析】(1)求出不等式的解,可得a的值,和A的坐标,根据象限点坐标的特征判断;(2)将a的值代入题中的方程组,可解得b,c的值,即求出了B的坐标,在坐标系中标出A,B,且AB于y轴交于C(0,2),即可解答;(3)由AB=MN,且AB//MN,可得AB通过平移可得到MN,则由点坐标平移的性质即可得到平移后,A与M对应,B与N对应或A与N对应,B与M对应。
【考点精析】通过灵活运用平行线的性质和坐标与图形变化-平移,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等即可以解答此题.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如下表:
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的 ![]() ,橱具店有哪几种进货方案?并说明理由.
,橱具店有哪几种进货方案?并说明理由.
(3)在(2)的条件下,直接写出橱具店赚钱最多的进货方案.