题目内容
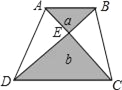
【题目】如图，梯形ABCD中，AB∥CD，两条对角线交于点E．已知△ABE的面积是a，△CDE的面积是b，则梯形ABCD的面积是（ ）
A. a2+b2 B. 
（a+b） C. 
D. （a+b）2
【答案】C
【解析】
由AB∥CD可得△ABE∽△CDE，由此可得
，则
，由此即可由△ABE的面积表达出△ADE的面积，同理可由△CDE的面积表达出△BCE的面积，这样由S梯形ABCD=S△ABE+S△ADE+S△CDE+S△BCE即可求出其面积的表达式了.
∵AB∥CD，
∴△ABE∽△CDE，
∵S△ABE=a，S△CDE=b，
∴，
∴，
∵△ABE边BE上的高和△ADE边DE上的高相等，
∴S△ABE：S△ADE=BE：DE，
∴S△ADE=
，
同理可得S△CBE=，
∴S梯形ABCD=S△ABE+S△ADE+S△CDE+S△BCE
=
=
.
故选C.
【题目】小明对某市出租汽车的计费问题进行研究，他搜集了一些资料，部分信息如下：
收费项目 | 收费标准 |
3公里以内收费 | 13元 |
基本单价 | 2.3元/公里 |
…… | …… |
备注：出租车计价段里程精确到500米；出租汽车收费结算以元为单位，元以下四舍五入。
小明首先简化模型，从简单情形开始研究：①只考虑白天正常行驶（无低速和等候）；②行驶路程3公里以上时，计价器每500米计价1次，且每1公里中前500米计价1.2元，后500米计价1.1元.
下面是小明的探究过程，请补充完整：
记一次运营出租车行驶的里程数为
（单位：公里），相应的实付车费为
（单位：元）.
（1）下表是y随x的变化情况
行驶里程数x | 0 | 0＜x＜3.5 | 3.5≤x＜4 | 4≤x＜4.5 | 4.5≤x＜5 | 5≤x＜5.5 | … |
实付车费y | 0 | 13 | 14 | 15 | … |
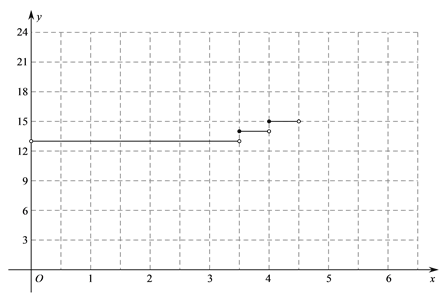
（2）在平面直角坐标系
中，画出当
时随变化的函数图象；
（3）一次运营行驶公里（
）的平均单价记为
（单位：元/公里），其中
.
①当
和
时，平均单价依次为
，则的大小关系是____________；（用“＜”连接）
②若一次运营行驶公里的平均单价不大于行驶任意
（
）公里的平均单价
，则称这次行驶的里程数为幸运里程数.请在上图中轴上表示出
（不包括端点）之间的幸运里程数的取值范围.