Question

【题目】【数学概念】

若四边形ABCD的四条边满足ABCDADBC，则称四边形ABCD是和谐四边形．

【特例辨别】

（1）下列四边形：①平行四边形，②矩形，③菱形，④正方形．其中一定是和谐四边形的是________．

【概念判定】

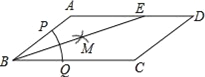
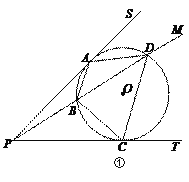
（2）如图①，过⊙O外一点P引圆的两条切线PS、PT，切点分别为A、C，过点P 作一条射线PM，分别交⊙O于点B、D，连接AB、BC、CD、DA．求证：四边形ABCD是和谐四边形．

【知识应用】

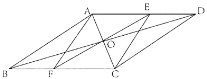
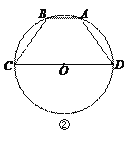
（3）如图②，CD是⊙O的直径，和谐四边形ABCD内接于⊙O，且BCAD．请直接写出AB与CD的关系．

Answer 1

【答案】③④

【解析】分析：（1）由于菱形和正方形的四条边相等，因此对边的乘积相等，所以菱形和正方形是和谐四边形；

（2）连接CO并延长，交⊙O于点E，连接BE．通过证明△PBC∽△PCD，得．同理，．由PA、PC为⊙O的切线，得PAPC，故，所以ABCDADBC，所以四边形ABCD是和谐四边形．

（3）AB∥CD ，CD3AB．

详解：（1）③④．

（2）证明：连接CO并延长，交⊙O于点E，连接BE．

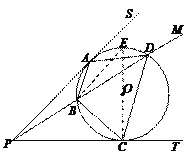
∵PT是⊙O的切线，切点为C，

∴∠PCE90°．

∴∠PCB∠ECB90°．

∵CE是⊙O的直径，

∴∠CBE90°，

∴∠BEC∠ECB90°，

∴∠BEC∠PCB．

又∵∠BEC∠BDC，∴∠PCB∠BDC．

又∵∠BPC∠CPD，∴△PBC∽△PCD，

∴．

同理，．

∵PA、PC为⊙O的切线，

∴PAPC，

∴．

∴ABCDADBC．

∴四边形ABCD是和谐四边形．

（3）AB∥CD ，CD3AB．