题目内容
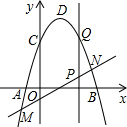 如图,在直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0)、B(3,0)两点,抛物线交y轴于点C(0,3),点D为抛物线的顶点.直线y=x-1交抛物线于点M、N两点,过线段MN上一点P作y轴的平行线交抛物线于点Q.
如图,在直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0)、B(3,0)两点,抛物线交y轴于点C(0,3),点D为抛物线的顶点.直线y=x-1交抛物线于点M、N两点,过线段MN上一点P作y轴的平行线交抛物线于点Q.(1)求此抛物线的解析式及顶点D的坐标;
(2)问点P在何处时,线段PQ最长,最长为多少;
(3)设E为线段OC上的三等分点,连接EP,EQ,若EP=EQ,求点P的坐标.
分析:(1)直接利用待定系数法将A、B、C的坐标代入抛物线y=ax2+bx+c(a≠0)就可以求出抛物线的解析式.
(2)根据抛物线的解析式和直线的解析式及PQ⊥x轴可以设出P点的横坐标,从而可以表示出P、Q的坐标,再利用P、Q的纵坐标之差表示出PQ的长,最后利用抛物线的最值就可以求出PQ的值及P点的坐标.
(3)由条件求出E点的坐标,再由条件表示出P、Q的坐标,然后根据两点间的距离公式就可以分情况求出点P的坐标.
(2)根据抛物线的解析式和直线的解析式及PQ⊥x轴可以设出P点的横坐标,从而可以表示出P、Q的坐标,再利用P、Q的纵坐标之差表示出PQ的长,最后利用抛物线的最值就可以求出PQ的值及P点的坐标.
(3)由条件求出E点的坐标,再由条件表示出P、Q的坐标,然后根据两点间的距离公式就可以分情况求出点P的坐标.
解答:解:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0)、B(3,0)两点,交y轴于点C(0,3),由题意,得
,
解得:
∴抛物线的解析式为:y=-x2+2x+3,
∴y=-(x-1)2+4,
∴D(1,4);
(2)∵PQ⊥x轴,
∴P、Q的横坐标相同,
∵P点在直线y=x-1上,设P(a,a-1),则Q(a,-a2+2a+3),
∴PQ=-a2+2a+3-a+1=-a2+a+4,
∴PQ=-(a-
)2+
,
∴当a=
时,线段PQ最长为
,则P点坐标为(
,-
);

(3)∵E为线段OC上的三等分点,且OC=3,
∴E(0,1)或E(0,2),
设P(p,p-1)(在y=x-1上),则Q(p,-p2+2p+3).
当E(0,1)时,
∵EP=EQ,
∴(p-0)2+(p-1-1)2=(p-0)2+(-p2+2p+3-1)2,
∴p2+(p-2)2=p2+(p2-2p-2)2,
(p-2)2=(p2-2p-2)2,
①当 p2-2p-2=p-2时,
∴p(p-3)=0,
∴p=0或3,
当p=0,P(0,-1),Q(0,3),
当p=3,P(3,2),Q(3,0),
过线段MN上一点P作y轴的平行线交抛物线于点Q.
∵直线y=x-1交抛物线于点M、N两点,
∴x-1=-x2+2x+3,
解得:x1=
,x2=
,
M的横坐标为
,N点的横坐标为
,
∴P点横坐标:大于等于
小于等于
,
∴P(3,2),Q(3,0)不符合要求舍去;
②p2-2p-2=-p+2,
整理得:p2-p-4=0,
解得:P1=
,p2=
,
∵直线y=x-1交抛物线于点M、N两点,
∴x-1=-x2+2x+3,
解得:x1=
,x2=
,
M的横坐标为
,N点的横坐标为
,
∵过线段MN上一点P作y轴的平行线交抛物线于点Q.
∴P点横坐标:大于等于
小于等于
,
当E(0,2)时,
∵EP=EQ,
∴(p-0)2+(p-1-2)2=(p-0)2+(-p2+2p+3-2)2,
p2+(p-3)2=p2+(p2-2p-1)2,
∴(p-3)2=(p2-2p-1)2.
③当 p2-2p-1=p-3时,
∴(p-1)(p-2)=0
∴p=1或2.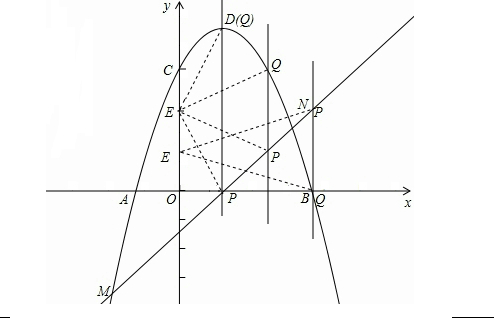
当p=1时,P(1,0),Q(1,4)
当p=2时,P(2,1),Q(2,3)
④p2-2p-1=-p+3
p2-p-4=0,
解得:P1=
<-1,p2=
>2,
P(
,
)或(
,
).
综上所述,P点的坐标为:P(0,-1),P(1,0),P(2,1),P(
,
)或(
,
).
∵点P在线段MN上,
∴P点的坐标为:P(0,-1),P(1,0),P(2,1).
|
解得:
|
∴抛物线的解析式为:y=-x2+2x+3,
∴y=-(x-1)2+4,
∴D(1,4);
(2)∵PQ⊥x轴,
∴P、Q的横坐标相同,
∵P点在直线y=x-1上,设P(a,a-1),则Q(a,-a2+2a+3),
∴PQ=-a2+2a+3-a+1=-a2+a+4,
∴PQ=-(a-
| 1 |
| 2 |
| 17 |
| 4 |
∴当a=
| 1 |
| 2 |
| 17 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |

(3)∵E为线段OC上的三等分点,且OC=3,
∴E(0,1)或E(0,2),
设P(p,p-1)(在y=x-1上),则Q(p,-p2+2p+3).
当E(0,1)时,
∵EP=EQ,
∴(p-0)2+(p-1-1)2=(p-0)2+(-p2+2p+3-1)2,
∴p2+(p-2)2=p2+(p2-2p-2)2,
(p-2)2=(p2-2p-2)2,
①当 p2-2p-2=p-2时,
∴p(p-3)=0,
∴p=0或3,
当p=0,P(0,-1),Q(0,3),
当p=3,P(3,2),Q(3,0),
过线段MN上一点P作y轴的平行线交抛物线于点Q.
∵直线y=x-1交抛物线于点M、N两点,
∴x-1=-x2+2x+3,
解得:x1=
1-
| ||
| 2 |
1+
| ||
| 2 |
M的横坐标为
1-
| ||
| 2 |
1+
| ||
| 2 |
∴P点横坐标:大于等于
1-
| ||
| 2 |
1+
| ||
| 2 |
∴P(3,2),Q(3,0)不符合要求舍去;
②p2-2p-2=-p+2,
整理得:p2-p-4=0,
解得:P1=
1-
| ||
| 2 |
1+
| ||
| 2 |
∵直线y=x-1交抛物线于点M、N两点,
∴x-1=-x2+2x+3,
解得:x1=
1-
| ||
| 2 |
1+
| ||
| 2 |
M的横坐标为
1-
| ||
| 2 |
1+
| ||
| 2 |
∵过线段MN上一点P作y轴的平行线交抛物线于点Q.
∴P点横坐标:大于等于
1-
| ||
| 2 |
1+
| ||
| 2 |
当E(0,2)时,
∵EP=EQ,
∴(p-0)2+(p-1-2)2=(p-0)2+(-p2+2p+3-2)2,
p2+(p-3)2=p2+(p2-2p-1)2,
∴(p-3)2=(p2-2p-1)2.
③当 p2-2p-1=p-3时,
∴(p-1)(p-2)=0
∴p=1或2.

当p=1时,P(1,0),Q(1,4)
当p=2时,P(2,1),Q(2,3)
④p2-2p-1=-p+3
p2-p-4=0,
解得:P1=
1-
| ||
| 2 |
1+
| ||
| 2 |
P(
1-
| ||
| 2 |
-
| ||
| 2 |
1+
| ||
| 2 |
| ||
| 2 |
综上所述,P点的坐标为:P(0,-1),P(1,0),P(2,1),P(
1-
| ||
| 2 |
-
| ||
| 2 |
1+
| ||
| 2 |
| ||
| 2 |
∵点P在线段MN上,
∴P点的坐标为:P(0,-1),P(1,0),P(2,1).
点评:本题是一道二次函数的综合试题,考查了待定系数法求二次函数的解析式,等腰三角形的判定及性质,两点间的距离公式的运用,二次函数最值的运用.

练习册系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: