题目内容
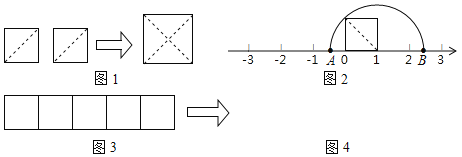
【题目】如图,已知数轴上点A表示的数为﹣1,点B表示的数为3,点P为数轴上一动点.
(1)点A到原点O的距离为 个单位长度;点B到原点O的距离为 个单位长度;线段AB的长度为 个单位长度;
(2)若点P到点A、点B的距离相等,则点P表示的数为 ;
(3)数轴上是否存在点P,使得PA+PB的和为6个单位长度?若存在,请求出PA的长;若不存在,请说明理由?
(4)点P从点A出发,以每分钟1个单位长度的速度向左运动,同时点Q从点B出发,以每分钟2个单位长度的速度向左运动,请直接回答:几分钟后点P与点Q重合?
![]()
【答案】(1)1,3,4;(2)1;(3)存在,PA=1;(4)经过4分钟后点P与点Q重合.
【解析】
(1)根据数轴上两点间的距离公式进行计算即可;
(2)设点P表示的数为x,根据题意列出方程可求解;
(3)设点P表示的数为y,分![]() ,
,![]() 和
和![]() 三种情况讨论,即可求解;
三种情况讨论,即可求解;
(4)设经过t分钟后点P与点Q重合,由点Q的路程﹣点P的路程=4,列出方程可求解.
解:(1)∵点A表示的数为﹣1,点B表示的数为3,
∴![]() ,
,![]() ,
,![]()
故答案为:1,3,4;
(2)设点P表示的数为x,
∵点P到点A、点B的距离相等,
∴![]()
∴x=1,
∴点P表示的数为1,
故答案为1;
(3)存在,
设点P表示的数为y,
当![]() 时,
时,
∵PA+PB=![]() ,
,
∴y=﹣2,
∴PA=![]() ,
,
当![]() 时,
时,
∵PA+PB=![]() ,
,
∴无解,
当y>3时,
∵PA+PB=![]() ,
,
∴y=4,
∴PA=5;
综上所述:PA=1或5.
(4)设经过t分钟后点P与点Q重合,
2t﹣t=4,
∴t=4
答:经过4分钟后点P与点Q重合.

练习册系列答案
相关题目