题目内容
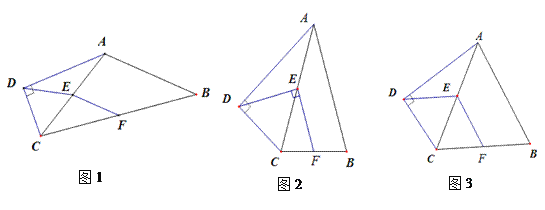
【题目】【问题原型】如图1,在四边形ABCD中,∠ADC=90°,AB=AC.点E、F分别为AC、BC的中点,连结EF,DE.试说明:DE=EF.
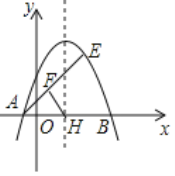
【探究】如图2,在问题原型的条件下,当AC平分∠BAD,∠DEF=90°时,求∠BAD的大小.
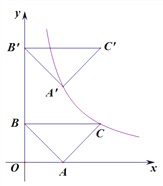
【应用】如图3,在问题原型的条件下,当AB=2,且四边形CDEF是菱形时,直接写出四边形ABCD的面积.
【答案】 【问题原型】详见解析;【探究】∠BAD=60°;【应用】![]()
【解析】试题分析:【问题原型】由三角形中位线定理和直角三角形斜边上的中线等于斜边的一半即可证明 .
【探究】先证明∠EDA=∠DAE=∠CAB=∠CEF,由外角的性质得到∠DEC=2∠DAC=2∠CEF,再由∠DEF=90°,得到∠CEF的度数,即可得到结论.
【应用】连接AF.证明△ECF是等边三角形,从而得到AD,AF的长,由S四边形ABCD=S△ADC+S△ABC=计算即可.
试题解析:解:【问题原型】
证明:在△ABC中,点E,F分别为AC,BC的中点,∴EF∥AB,且EF=![]() AB .
AB .
在Rt△ACD中,点E为AC的中点,∴DE=![]() AC.∵AB=AC,∴DE=EF .
AC.∵AB=AC,∴DE=EF .
【探究】
∵AC平分∠BAD,EF∥AB,DE=![]() AC=AE=EC ,∴∠BAC=∠DAC,∠CEF=∠BAC,
AC=AE=EC ,∴∠BAC=∠DAC,∠CEF=∠BAC,
∠DEC=2∠DAC=∠BAD.∵∠DEF=90°,∴∠CEF+∠DEC=∠BAC+2∠DAC=90°,∴∠BAC=∠DAC=30°,∴∠BAD=60° .
【应用】
连接AF.∵AC=AB,F为BC的中点,∴AF⊥BC.∵四边形CDEF是菱形,∴CF=EF=DE=DC.∵DE=EC=EF=1,∴EC=EF=CF=1,∴△ECF是等边三角形,∴∠ECF=60°,∴∠DCE=60°,∴∠DAC=30°,∴AD=![]() DC=
DC=![]() ,AF=
,AF=![]() CF=
CF=![]() .∴S四边形ABCD=S△ADC+S△ABC=
.∴S四边形ABCD=S△ADC+S△ABC=![]() ADDC+
ADDC+![]() CBAF=
CBAF=![]() =
=![]() .
.

 考前必练系列答案
考前必练系列答案