题目内容
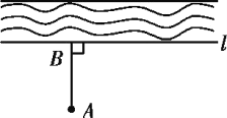
【题目】(1)如图,要把小河里的水引到田地A处,就作AB⊥l(垂足为B),沿AB挖水沟,水沟最短.理由是___________.
(2)把命题“平行于同一直线的两直线平行”写成“如果……,那么……”的形式._____________________________ .
(3)比较大小:![]() ______
______ ![]() .
.
(4)已知![]() 与
与![]() 是同类项,则m-3n的平方根是___.
是同类项,则m-3n的平方根是___.
(5)已知点P的坐标为(3a+6,2﹣a),且点P到两坐标轴的距离相等,则点P的坐标是______.
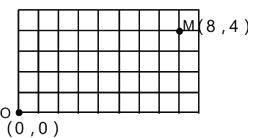
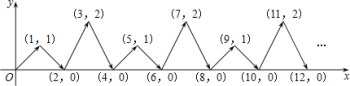
(6) 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2018次运动后,动点P的坐标是______________
【答案】垂线段最短 如果两条直线都和同一条直线平行,那么这两条直线也互相平行 < ±6 (3,3)或(-6,6) (2018,0)
【解析】
(1)根据垂线段最短解答;
(2)根据命题的形式解答即可;
(3)先化简![]() 即可相比较得到答案;
即可相比较得到答案;
(4)根据同类项的定义得到m、n,即可得到答案;
(5)根据点到坐标轴的距离列方程解答即可;
(6)根据图形发现点是按照四次一循环的规律变化的,找到点坐标的变化规律即可得到答案.
(1)∵AB⊥直线l,
∴AB最短,
理由是:垂线段最短,
故答案为:垂线段最短;
(2)把命题“平行于同一直线的两直线平行”写成“如果……,那么……”的形式是如果两条直线都和第三条直线平行,那么这两条直线也互相平行,
故答案为:如果两条直线都和第三条直线平行,那么这两条直线也互相平行;
(3)∵![]() =
=![]() ,且
,且![]() <
<![]() ,
,
∴![]() <
<![]() ,
,
故答案为:<;
(4)∵![]() 与
与![]() 是同类项,
是同类项,
∴m-2=4,2m+n=2,
∴m=6,n=-10,
∴m-3n=6+30=36,
∴m-3n的平方根是![]() ,
,
故答案为:![]() ;
;
(5)∵点P的坐标为(3a+6,2﹣a),且点P到两坐标轴的距离相等,
∴![]() ,
,
∴![]() 或
或![]() ,
,
∴a=-1或a=-4;
当a=-1时,点P的坐标是(3,3),
当a=-4时,点P的坐标是(-6,6),
故答案为:(3,3)或(-6,6);
(6)第1次运动到点(1,1),
第2次运动到点(2,0),
第3次运动到点(3,2),
第4次运动到点(4,0),
第5次运动到点(5,1),
第6次运动到点(6,0),
第7次运动到点(7,2)
第8次运动到点(8,0),
![]() ,
,
由此得到规律:图形每4次变化一次,且点的横坐标与点运动的次数相同,纵坐标依次是1、0、2、0循环变化,
∵![]() ,
,
∴经过第2018次运动后,动点P的坐标是(2018,0),
故答案为:(2018,0).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案