题目内容
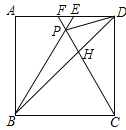
【题目】如图1,在△ABC中,AE⊥BC于点E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.
(1)试判断BD与AC的位置关系和数量关系,并说明理由;
(2)如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由.

【答案】(1)BD⊥AC,BD=AC(2)BD⊥AC,BD=AC
【解析】试题分析:
(1)延长BD交AC于点F,用SAS证明△BDE≌△ACE即可解题;
(2)用SAS证明△BDE≌△ACE可得BD=AC,再证∠AFB=90°即可.
(1)BD⊥AC,BD=AC.
试题解析:
证明:延长BD交AC于点F. ∵AE⊥BC于点E, ∴∠BED=∠AEC=90°.又AE=BE,DE=CE, ∴△DBE≌△CAE(SAS). ∴BD=AC, ∠DBE=∠CAE,∠BDE=∠ACE. ∵∠BDE=∠ADF, ∴ ∠ADF=∠ACE. ∵∠ACE+∠CAE=90°, ∴∠ADF+∠CAE=90°. ∴BD⊥AC.
(2)BD⊥AC,BD=AC.
证明: ∵∠AEB=∠DEC=90°, ∴∠AEB+∠AED=∠DEC+∠AED,即∠BED=∠AEC.又AE=BE,DE=CE, ∴△DBE≌△CAE(SAS). ∴BD=AC, ∠DBE=∠CAE,∠BDE=∠ACE. ∵∠BFC=∠ACD+∠CDE +∠BDE=∠ACD+∠CDE +∠ACE=∠ECD+∠CDE=90°, ∴BD⊥AC.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目