Question

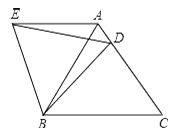
【题目】如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连接BD、DP，BD与CF相交于点H．给出下列结论：

①△ABE≌△DCF；②；③DP2=PHPB；④．

其中正确的是____________．（写出所有正确结论的序号）

Answer 1

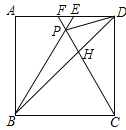
【答案】①③④．

【解析】试题分析：∵△BPC是等边三角形，∴BP=PC=BC，∠PBC=∠PCB=∠BPC=60°，在正方形ABCD中，∵AB=BC=CD，∠A=∠ADC=∠BCD=90°，∴∠ABE=∠DCF=30°，在△ABE与△CDF中，∵∠A=∠ADC，∠ABE=∠DCF，AB=CD，∴△ABE≌△DCF，故①正确；

∵PC=CD，∠PCD=30°，∴∠PDC=75°，∴∠FDP=15°，∵∠DBC=45°，∴∠PBD=15°，∴∠FDP=∠PBD，∵∠DFP=∠BPC=60°，∴△DFP∽△BPH，∴，故②错误；

∵∠PDH=∠PCD=30°，∵∠DPH=∠DPC，∴△DPH∽△CPD，∴，∴，∵PB=CD，∴，故③正确；

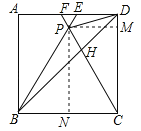
如图，过P作PM⊥CD，PN⊥BC，设正方形ABCD的边长是4，△BPC为正三角形，∴∠PBC=∠PCB=60°，PB=PC=BC=CD=4，∴∠PCD=30°∴PN=PBsin60°=4×=，PM=PCsin30°=2，S△BPD=S四边形PBCD﹣S△BCD=S△PBC+S△PDC﹣S△BCD=，∴．故答案为：①③④．