题目内容
【题目】如图,正方形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() .
.
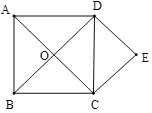
(1)求证:四边形![]() 是正方形.
是正方形.
(2)若![]() ,则点
,则点![]() 到边
到边![]() 的距离为______.
的距离为______.
【答案】(1)证明见解析;(2)1.5.
【解析】
(1)首先根据已知条件可判定四边形OCED是平行四边形,然后根据正方形对角线互相平分的性质,可判定四边形OCED是菱形,又根据正方形的对角线互相垂直,即可判定四边形OCED是正方形;
(2)首先连接EO,并延长EO交AB于点F,根据已知条件和(1)的结论,可判定EF即为点E到AB的距离,即为EO和OF之和,根据勾股定理,可求出AD和CD,即可得解.
解:(1)∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是正方形,
∴AC=BD, ,
∴OC=OD.
∴四边形OCED是菱形.
∵AC⊥BD,
∴∠COD=90°.
∴四边形OCED是正方形.
(2)解:连接EO,并延长EO交AB于点F,如图所示
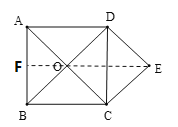
由(1)中结论可得,OE=CD
又∵正方形ABCD,![]() ,AD=CD,OF⊥AB
,AD=CD,OF⊥AB
∴![]()
∴AD=CD=1,
∴![]()
∴![]()
EF即为点E到AB的距离,
故答案为1.5.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
【题目】要从甲、乙两名同学中选出一名,代表班级参加射击比赛. 现将甲、乙两名同学参加射击训练的成绩绘制成下列两个统计图:
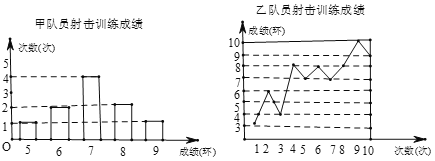
根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差( | |
甲 | 7 |
| 7 | 1. 2 |
乙 |
| 7. 5 |
| 4. 2 |
(1)分别求表格中![]() 、
、![]() 、
、![]() 的值.
的值.
(2)如果其他参赛选手的射击成绩都在7环左右,应该选______队员参赛更适合;如果其他参赛选手的射击成绩都在8环左右,应该选______队员参赛更适合.