题目内容
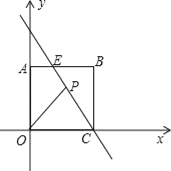
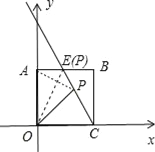
【题目】如图,已知点C(4,0)是正方形AOCB的一个顶点,直线PC交AB于点E,若E是AB的中点.
(1)求点E的坐标;
(2)求直线PC的解析式;
(3)若点P是直线PC在第一象限的一个动点,当点P运动到什么位置时,图中存在与△AOP全等的三角形?请求出P点的坐标,并说明理由.
【答案】(1)点E的坐标为(2,4);(2)直线PC的解析式为y=﹣2x+8;(3)点P坐标为(2,4)或(![]() ,
, ![]() ).
).
【解析】试题分析:(1)因为E是AB中点,计算出A和B的坐标即可算出E的坐标;
(2)根据E和C的坐标即可求出直线PC的解析式;
(3)根据全等三角形的判定方法,找出全部的点P即可.
试题解析:(1)∵四边形AOCB是正方形,C(4,0),∴点B(4,4),C(4,0),
∵E是AB的中点,∴点E的坐标为(2,4).
(2)设直线PC的解析式为y=kx+b,将点E(2,4)、C(4,0)代入y=kx+b中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴直线PC的解析式为y=﹣2x+8.
(3)有两种情况,如图所示.
①当点P与点E重合时,
在△OAE和△CBE中, 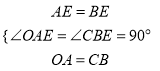 ,∴△OAE≌△CBE(SAS),
,∴△OAE≌△CBE(SAS),
此时点P坐标为(2,4);
②当AP等于CP时,
在△AOP和△COP中, 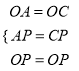 ,∴△AOP≌△COP(SSS),∴∠AOP=∠COP=45°,
,∴△AOP≌△COP(SSS),∴∠AOP=∠COP=45°,
∴直线OP的解析式为y=x.
联立直线OP、PC的解析式得: ![]() ,解得:
,解得: 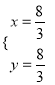 ,
,
∴此时点P的坐标为(![]() ,
, ![]() ).
).

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】为促进朗诵艺术的普及、发展,挖掘播音主持人才,某校初二年级举办朗诵大赛,凡凡同学根据比赛中九位评委所给的某位参赛选手的分数,制作了一个表格,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
中位数 | 众数 | 平均数 | 方差 |
9.2 | 9.3 | 9.1 | 0.3 |
A.中位数
B.众数
C.平均数
D.方差