题目内容
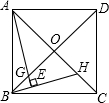
如图,正方形ABCD的两条对角线交于点O.
(1)若H为OC上一点,过A作BH的垂线,垂足为E,AE与BO相交于点G.试探索OH与OG的数量关系,并证明;
(2)若点H在OC的延长线上,过A作BH的垂线,交HB的延长线于点E,直线AE与OB相交于点G.(1)中的结论还成立吗?若成立,给出证明;若不成立,请说明理由.
解:(1)OH=OG.
证明:∵四边形ABCD为正方形,
∴AO=B0,B0⊥AC(正方形两条对角线相等,互相垂直平分),
∴∠AOG=∠BOH=90°,(2分)
则∠OAG+∠OGA=90°,又AE⊥BH,
∴∠AEB=90°,则∠OBH+∠BGE=90°,
而∠OGA=∠BGE,
∴∠OAG=∠OBH,(4分)
∴△OAG≌△OBH(ASA),
则OH=OG;(6分)

(2)OH=OG成立.(无此步不扣分)(7分)
证明:∵四边形ABCD为正方形,
∴AO=BO,BO⊥AC,
∴∠AOG=∠BOH=90°(8分)
则∠H+∠HBO=90°,又AE⊥BH,
∴∠GEB=90°,则∠G+∠GBE=90°,
又∠HBO=∠GBE,
∴∠H=∠G(9分)
∴△AOG≌△BOH.(AAS)
则OG=OH.(11分)
分析:(1)根据正方形的性质对角线垂直且平分,得到OB与OA相等且垂直,又因为AG垂直于BH,根据直角三角形的两锐角互余得到:∠OAG+∠OGA=90°,∠OBH+∠BGE=90°,再根据等角的余角相等得到∠OAG=∠OBH,从而利用“ASA”证出Rt△BOH≌Rt△AOG,由全等三角形的对应边相等得到OG=OH;
(2)根据正方形的性质得到OB与OA相等且垂直,根据直角三角形的两锐角互余得到:∠H+∠HBO=90°,∠G+∠EBG=90°,再根据等角的余角相等得到∠G=∠H,从而利用“AAS”证出Rt△BOH≌Rt△AOG,由全等三角形的对应边相等得到OG=OH.
点评:本题考查正方形的性质,以及三角形全等的判定与性质,是一道结论探索性问题.解答此类题我们要从变化中探究不变的数学本质,再从不变的数学本质出发,寻求变化的规律,通过观察、试验、归纳、类比等获得数学猜想,并对所作的猜想进行严密的逻辑论证,考查了学生对知识的迁移能力,分析问题、解决问题的能力.
证明:∵四边形ABCD为正方形,
∴AO=B0,B0⊥AC(正方形两条对角线相等,互相垂直平分),
∴∠AOG=∠BOH=90°,(2分)
则∠OAG+∠OGA=90°,又AE⊥BH,
∴∠AEB=90°,则∠OBH+∠BGE=90°,
而∠OGA=∠BGE,
∴∠OAG=∠OBH,(4分)
∴△OAG≌△OBH(ASA),
则OH=OG;(6分)

(2)OH=OG成立.(无此步不扣分)(7分)
证明:∵四边形ABCD为正方形,
∴AO=BO,BO⊥AC,
∴∠AOG=∠BOH=90°(8分)
则∠H+∠HBO=90°,又AE⊥BH,
∴∠GEB=90°,则∠G+∠GBE=90°,
又∠HBO=∠GBE,
∴∠H=∠G(9分)
∴△AOG≌△BOH.(AAS)
则OG=OH.(11分)
分析:(1)根据正方形的性质对角线垂直且平分,得到OB与OA相等且垂直,又因为AG垂直于BH,根据直角三角形的两锐角互余得到:∠OAG+∠OGA=90°,∠OBH+∠BGE=90°,再根据等角的余角相等得到∠OAG=∠OBH,从而利用“ASA”证出Rt△BOH≌Rt△AOG,由全等三角形的对应边相等得到OG=OH;
(2)根据正方形的性质得到OB与OA相等且垂直,根据直角三角形的两锐角互余得到:∠H+∠HBO=90°,∠G+∠EBG=90°,再根据等角的余角相等得到∠G=∠H,从而利用“AAS”证出Rt△BOH≌Rt△AOG,由全等三角形的对应边相等得到OG=OH.
点评:本题考查正方形的性质,以及三角形全等的判定与性质,是一道结论探索性问题.解答此类题我们要从变化中探究不变的数学本质,再从不变的数学本质出发,寻求变化的规律,通过观察、试验、归纳、类比等获得数学猜想,并对所作的猜想进行严密的逻辑论证,考查了学生对知识的迁移能力,分析问题、解决问题的能力.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
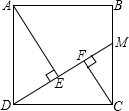 19、如图:正方形ABCD,M是线段BC上一点,且不与B、C重合,AE⊥DM于E,CF⊥DM于F.求证:AE2+CF2=AD2.
19、如图:正方形ABCD,M是线段BC上一点,且不与B、C重合,AE⊥DM于E,CF⊥DM于F.求证:AE2+CF2=AD2.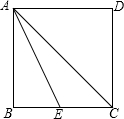 如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE=
如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE=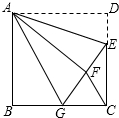 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( ) 17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是
17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是 如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.
如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.