题目内容
如图,抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C.大圆的圆心是该抛物线的顶点D,小圆的圆心是该抛物线与x轴正半轴的交点B,大圆与x轴相切于点E,小圆与y轴相切于点O,两圆外切于点F,大圆半径 R是小圆半径r的4倍.
R是小圆半径r的4倍.
(1)求ac+b的值;
(2)在抛物线上找点P,使△PAO能与△EBF相似(用含r的代数式表示点P的坐标,并证明△PAO与△EBF相似).
 R是小圆半径r的4倍.
R是小圆半径r的4倍.(1)求ac+b的值;
(2)在抛物线上找点P,使△PAO能与△EBF相似(用含r的代数式表示点P的坐标,并证明△PAO与△EBF相似).
分析:(1)连接DE.设⊙B、⊙D的半径分别为r、R,根据切线的性质得出DE⊥x轴于E,先用含r的代数式分别表示点A,B,D的坐标,再运用待定系数法求出经过A,B,D的解析式,得出a、b、c的值,代入即可求出ac+b的值;
(2)先在抛物线上找出点P,再证明△PAO与△EBF相似.为此,过点A作AP∥BD,交抛物线于点P,先运用待定系数法求出直线AP的解析式,再与(1)中求出的抛物线的解析式联立,得到方程组,解方程组求出交点P的坐标,然后通过计算得出AO:BF=AP:EB=5,又∠PAO=∠EBF,根据两组对应边的比相等且夹角相等的两三角形相似得出△PAO∽△EBF.
(2)先在抛物线上找出点P,再证明△PAO与△EBF相似.为此,过点A作AP∥BD,交抛物线于点P,先运用待定系数法求出直线AP的解析式,再与(1)中求出的抛物线的解析式联立,得到方程组,解方程组求出交点P的坐标,然后通过计算得出AO:BF=AP:EB=5,又∠PAO=∠EBF,根据两组对应边的比相等且夹角相等的两三角形相似得出△PAO∽△EBF.
解答: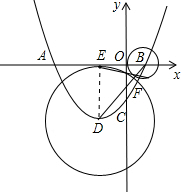 解:(1)连接DE.设⊙B、⊙D的半径分别为r、R(r>0,R>0),则有DE⊥x轴于E,且R=4r.
解:(1)连接DE.设⊙B、⊙D的半径分别为r、R(r>0,R>0),则有DE⊥x轴于E,且R=4r.
∴ED=4r,DB=5r,∴EB=AE=3r,
∴OE=2r,AO=5r,
∴A(-5r,0),B(r,0),D(-2r,-4r).
设y=a(x+2r)2-4r,将B(r,0)代入,
得0=a(r+2r)2-4r,
解得a=
,
∴y=
(x+2r)2-4r,即y=
x2+
x-
r,
∴ac+b=
×(-
r)+
=
;
 (2)过点A作AP∥BD,交抛物线于点P,连接PO、EF,则点P即为所求.
(2)过点A作AP∥BD,交抛物线于点P,连接PO、EF,则点P即为所求.
由B(r,0),D(-2r,-4r),
运用待定系数法求出直线BD的解析式为y=
x-
r,
∵AP∥BD,∴可设直线AP的解析式为y=
x+n,
将A(-5r,0)代入,得0=
×(-5r)+n,
解得n=
r,
∴直线AP的解析式为y=
x+
r.
解方程组
,
解得
,
(与A点重合,舍去).
∴P点的坐标为(4r,12r),
∵A(-5r,0),∴AP=
=15r,
∵AO=5r,BF=r,EB=3r,∴AO:BF=AP:EB=5,
∵AP∥BD,∴∠PAO=∠EBF,
∴△PAO∽△EBF.
 解:(1)连接DE.设⊙B、⊙D的半径分别为r、R(r>0,R>0),则有DE⊥x轴于E,且R=4r.
解:(1)连接DE.设⊙B、⊙D的半径分别为r、R(r>0,R>0),则有DE⊥x轴于E,且R=4r.∴ED=4r,DB=5r,∴EB=AE=3r,
∴OE=2r,AO=5r,
∴A(-5r,0),B(r,0),D(-2r,-4r).
设y=a(x+2r)2-4r,将B(r,0)代入,
得0=a(r+2r)2-4r,
解得a=
| 4 |
| 9r |
∴y=
| 4 |
| 9r |
| 4 |
| 9r |
| 16 |
| 9 |
| 20 |
| 9 |
∴ac+b=
| 4 |
| 9r |
| 20 |
| 9 |
| 16 |
| 9 |
| 64 |
| 81 |
 (2)过点A作AP∥BD,交抛物线于点P,连接PO、EF,则点P即为所求.
(2)过点A作AP∥BD,交抛物线于点P,连接PO、EF,则点P即为所求.由B(r,0),D(-2r,-4r),
运用待定系数法求出直线BD的解析式为y=
| 4 |
| 3 |
| 4 |
| 3 |
∵AP∥BD,∴可设直线AP的解析式为y=
| 4 |
| 3 |
将A(-5r,0)代入,得0=
| 4 |
| 3 |
解得n=
| 20 |
| 3 |
∴直线AP的解析式为y=
| 4 |
| 3 |
| 20 |
| 3 |
解方程组
|
解得
|
|
∴P点的坐标为(4r,12r),
∵A(-5r,0),∴AP=
| (4r+5r)2+(12r)2 |
∵AO=5r,BF=r,EB=3r,∴AO:BF=AP:EB=5,
∵AP∥BD,∴∠PAO=∠EBF,
∴△PAO∽△EBF.
点评:本题考查了直线与圆、圆与圆的位置关系,运用待定系数法求一次函数、二次函数的解析式,平面直角坐标系中交点坐标的求法,相似三角形的判定,本题综合性较强,难度较大,需认真观察图形,正确地作出辅助线.

练习册系列答案
相关题目
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).