ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΨΊ–Έ![]() ÷–Θ§
÷–Θ§![]() ΈΣ‘≠ΒψΘ§Βψ
ΈΣ‘≠ΒψΘ§Βψ![]() ‘Ύ
‘Ύ![]() ÷α…œΘ§Βψ
÷α…œΘ§Βψ![]() ‘Ύ
‘Ύ![]() ÷α…œΘ§Βψ
÷α…œΘ§Βψ![]() ΒΡΉχ±ξΈΣΘ®4,3Θ©Θ§≈ΉΈοœΏ
ΒΡΉχ±ξΈΣΘ®4,3Θ©Θ§≈ΉΈοœΏ![]() ”κ
”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§”κ÷±œΏ
Θ§”κ÷±œΏ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§”κ
Θ§”κ![]() ÷αΫΜ”Ύ
÷αΫΜ”Ύ![]() ΝΫΒψ.
ΝΫΒψ.
Θ®1Θ©«σ≈ΉΈοœΏΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©Βψ![]() ¥”Βψ
¥”Βψ![]() ≥ωΖΔΘ§‘ΎœΏΕΈ
≥ωΖΔΘ§‘ΎœΏΕΈ![]() …œ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρΒψ
…œ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρΒψ![]() ‘ΥΕ·Θ§”κ¥ΥΆ§ ±Θ§Βψ
‘ΥΕ·Θ§”κ¥ΥΆ§ ±Θ§Βψ![]() ¥”Βψ
¥”Βψ![]() ≥ωΖΔΘ§‘ΎœΏΕΈ
≥ωΖΔΘ§‘ΎœΏΕΈ![]() …œ“‘ΟΩΟκ
…œ“‘ΟΩΟκ![]() ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρΒψ
ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρΒψ![]() ‘ΥΕ·Θ§Β±Τδ÷–“ΜΒψΒΫ¥ο÷’Βψ ±Θ§Νμ“ΜΒψ“≤ΆΘ÷Ι‘ΥΕ·.Ν§Ϋ”
‘ΥΕ·Θ§Β±Τδ÷–“ΜΒψΒΫ¥ο÷’Βψ ±Θ§Νμ“ΜΒψ“≤ΆΘ÷Ι‘ΥΕ·.Ν§Ϋ”![]() Θ§…η‘ΥΕ· ±ΦδΈΣ
Θ§…η‘ΥΕ· ±ΦδΈΣ![]() Θ®ΟκΘ©.
Θ®ΟκΘ©.
ΔΌΒ±![]() ΈΣΚΈ÷Β ±Θ§
ΈΣΚΈ÷Β ±Θ§![]() ΒΟΟφΜΐΉν–ΓΘΩ
ΒΟΟφΜΐΉν–ΓΘΩ
ΔΎ «Ζώ¥φ‘ΎΡ≥“Μ ±ΩΧ![]() Θ§ Ι
Θ§ Ι![]() ΈΣ÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§÷±Ϋ”–¥≥ω
ΈΣ÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§÷±Ϋ”–¥≥ω![]() ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©ΔΌ
ΘΜΘ®2Θ©ΔΌ ![]() ΘΜΔΎ
ΘΜΔΎ![]()
ΓΨΫβΈωΓΩ
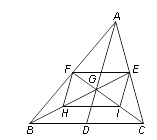
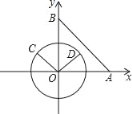
Θ®1Θ©ΗυΨίΒψBΒΡΉχ±ξΩ…ΒΟ≥ωΒψAΘ§CΒΡΉχ±ξΘ§¥ζ»κ≈ΉΈοœΏΫβΈω ΫΦ¥Ω…«σ≥ωbΘ§cΒΡ÷ΒΘ§«σΒΟ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
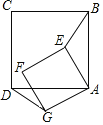
Θ®2Θ©ΔΌΙΐΒψQΓΔPΉςQFΓΆABΓΔPGΓΆACΘ§¥ΙΉψΖ÷±πΈΣFΓΔGΘ§ΆΤ≥ωΓςQFAΓΉΓςCBAΘ§ΓςCGPΓΉΓςCBAΘ§”ΟΚ§tΒΡ ΫΉ”±μ ΨOFΘ§PGΘ§ΫΪ»ΐΫ«–ΈΒΡΟφΜΐ”ΟΚ§tΒΡ ΫΉ”±μ Ψ≥ωά¥Θ§ΫαΚœΕΰ¥ΈΚ· ΐΒΡ–‘÷ Ω…«σ≥ωΉν÷ΒΘΜΔΎ”…”Ύ»ΐΫ«–Έ÷±Ϋ«ΒΡΈΜ÷Ο≤Μ»ΖΕ®Θ§–ηΖ÷«ιΩωΧ÷¬έΘ§ΗυΨίΒψΒΡΉχ±ξΘ§‘ΌΫαΚœΝΫΒψΦδΒΡΨύάκΙΪ Ϋ”ΟΙ¥Ι…Ε®άμ«σΫβΦ¥Ω…Θ°
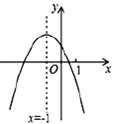
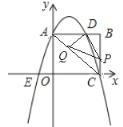
ΫβΘΚΘ®1Θ©”…Χβ“β÷ΣΘΚA(0,3),C(4,0)Θ§
ΓΏ≈ΉΈοœΏΨ≠ΙΐAΓΔBΝΫΒψΘ§
Γύ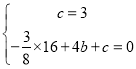 Θ§ΫβΒΟΘ§
Θ§ΫβΒΟΘ§![]() Θ§
Θ§
Γύ≈ΉΈοœΏΒΡ±μ¥ο ΫΈΣΘΚ![]() Θ°
Θ°
(2)ΔΌ ΓΏΥΡ±Ώ–ΈABCD «ΨΊ–ΈΘ§
ΓύΓœB=90OΘ§ ΓύAC2=AB2+BC2=5ΘΜ
”…![]() Θ§Ω…ΒΟ
Θ§Ω…ΒΟ![]() Θ§ΓύDΘ®2,3Θ©Θ°
Θ§ΓύDΘ®2,3Θ©Θ°
ΙΐΒψQΓΔPΉςQFΓΆABΓΔPGΓΆACΘ§¥ΙΉψΖ÷±πΈΣFΓΔGΘ§
ΓΏΓœFAQ=ΓœBACΘ§ ΓœQFA=ΓœCBAΘ§
ΓύΓςQFAΓΉΓςCBAΘ°
Γύ![]() Θ§
Θ§
Γύ![]() Θ°
Θ°
Ά§άμΘΚΓςCGPΓΉΓςCBAΘ§
Γύ![]() Γύ
Γύ![]() Θ§Γύ
Θ§Γύ![]() Θ§
Θ§
![]()
![]()
Β±![]() ±Θ§ΓςDPQΒΡΟφΜΐΉν–Γ.Ήν–Γ÷ΒΈΣ
±Θ§ΓςDPQΒΡΟφΜΐΉν–Γ.Ήν–Γ÷ΒΈΣ![]() Θ°
Θ°
ΔΎ ”…ΆΦœώΩ…÷ΣΒψDΒΡΉχ±ξΈΣ(2,3)Θ§AC=5,÷±œΏACΒΡΫβΈω ΫΈΣΘΚ![]() Θ°
Θ°
»ΐΫ«–Έ÷±Ϋ«ΒΡΈΜ÷Ο≤Μ»ΖΕ®Θ§–ηΖ÷«ιΩωΧ÷¬έΘΚ
Β±![]() ±Θ§ΗυΨίΙ¥Ι…Ε®άμΩ…ΒΟ≥ωΘΚ
±Θ§ΗυΨίΙ¥Ι…Ε®άμΩ…ΒΟ≥ωΘΚ
![]() Θ§
Θ§
’ϊάμΘ§ΫβΖΫ≥ΧΦ¥Ω…ΒΟΫβΘΜ
Β±![]() ±Θ§Ω…÷ΣΒψG‘ΥΕ·ΒΫΒψBΒΡΈΜ÷ΟΘ§ΒψP‘ΥΕ·ΒΫCΒΡΈΜ÷ΟΘ§Υυ–η ±ΦδΈΣt=3ΘΜ
±Θ§Ω…÷ΣΒψG‘ΥΕ·ΒΫΒψBΒΡΈΜ÷ΟΘ§ΒψP‘ΥΕ·ΒΫCΒΡΈΜ÷ΟΘ§Υυ–η ±ΦδΈΣt=3ΘΜ
Β±![]() ±,Ά§άμ”ΟΙ¥Ι…Ε®άμΒΟ≥ωΘΚ
±,Ά§άμ”ΟΙ¥Ι…Ε®άμΒΟ≥ωΘΚ
![]() ΘΜ
ΘΜ
’ϊάμ«σΫβΩ…ΒΟtΒΡ÷ΒΘ°
”…¥ΥΩ…ΒΟ≥ωtΒΡ÷ΒΈΣΘΚ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() Θ°
Θ°

 ÷«»Λ νΦΌΈ¬Ι ÷Σ–¬œΒΝ–¥πΑΗ
÷«»Λ νΦΌΈ¬Ι ÷Σ–¬œΒΝ–¥πΑΗ ”Δ”ο–Γ”Δ–έΧλΧλΡ§–¥œΒΝ–¥πΑΗ
”Δ”ο–Γ”Δ–έΧλΧλΡ§–¥œΒΝ–¥πΑΗ νΦΌΉς“ΒΑ≤Μ’…ΌΡξΕυΆ·≥ωΑφ…γœΒΝ–¥πΑΗ
νΦΌΉς“ΒΑ≤Μ’…ΌΡξΕυΆ·≥ωΑφ…γœΒΝ–¥πΑΗ