题目内容
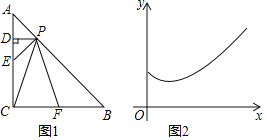
【题目】如图，直线l上有两动点C、D，点A、点B在直线l同侧，且A点与B点分别到l的距离为a米和b米（即图中AA′=a米，BB′=b米），且A′B′=c米，动点CD之间的距离总为S米，使C到A的距离与D到B的距离之和最小，则AC+BD的最小值为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
作线段AP∥L且AP=S，且点P在点A的右侧，作P关于L的对称点P′，连接BP′交直线L于点D，在L上D的左侧截取DC=S，此时BP′即为所求的最小值，作P′E⊥BB′交BB′的延长线于E，利用勾股定理求解即可．
解：作线段AP∥L且AP=S，且点P在点A的右侧，作P关于L的对称点P′，连接BP′交直线L于点D，
∵P′E=c-S，BE=a+b，
∴P′B=
=
.
故选：D．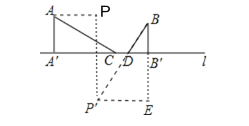
练习册系列答案
阅读快车系列答案
相关题目
【题目】九年级数学兴趣小组经过市场调查，得到某种运动服每月的销量是售价的一次函数，且相关信息如下表：
售价（元/件） | 100 | 110 | 120 | 130 | … |
月销量（件） | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元，设售价为x元．
（1）请用含x的式子表示：①销售该运动服每件的利润是（ ）元；
（2）求月销量y与售价x的一次函数关系式：
（3）设销售该运动服的月利润为W元，那么售价为多少元时，当月的利润最大？最大利润是多少元？
