Question

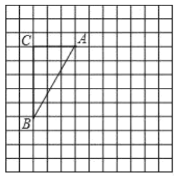
【题目】证明：如果四边形两条对角线相等，那么以它的四边中点为顶点可组成一个菱形.

Answer 1

【答案】证明见解析.

【解析】

先写出命题的已知和求证，根据三角形的中位线定理得出EF∥BD，GH∥BD，EF=BD，GH=BD，EH=AC，由平行于同一直线的两直线平行得出EF∥GH，由等式的性质得出EF=GH，根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形，又由AC=BD及EF=BD，EH=AC，得出EF=EH，根据有一组邻边相等的平行四边形是菱形得出平行四边形EFGH是菱形．

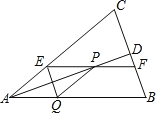
已知，四边形ABCD中，AC=BD，E、F、G、H分别是边AD、AB、BC、CD的中点，连接EF、FG、GH、HE，得到四边形EFGH．

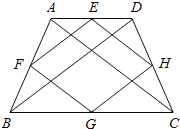
求证：四边形EFGH是菱形.

证明：∵E、F、G、H分别是边AD、AB、BC、CD的中点，

∴EF∥BD，GH∥BD，EF=BD，GH=BD，EH=AC，

∴EF∥GH，EF=GH，

∴四边形EFGH是平行四边形，

∵AC=BD，EF=BD，EH=AC，

∴EF=EH，

∴平行四边形EFGH是菱形．