题目内容
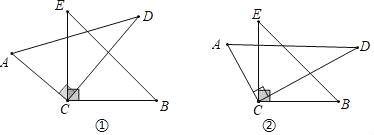
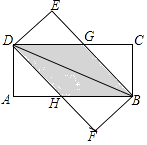
【题目】如图,在四边形ABCD中,∠DAB=∠BCD=90°,点E是BD上任意一点,点O是AC的中点,AF∥EC交EO的延长线于点F,连接AE,CF.
(1)判断四边形AECF是什么四边形,并证明;
(2)若点E是BD的中点,四边形AECF又是什么四边形?说明理由.
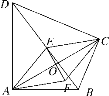
【答案】(1)四边形AECF是平行四边形.证明见解析;(2)四边形AECF是菱形.理由见解析.
【解析】
(1)由ASA证明△AOF≌△COE,得出OF=OE,即可得出结论;
(2)由直角三角形斜边上的中线性质得出AE=![]() BD,CE=
BD,CE=![]() BD,得出AE=CE,即可得出结论.
BD,得出AE=CE,即可得出结论.
(1)四边形AECF是平行四边形.
证明如下:∵点O是AC的中点,
∴AO=CO.∵AF∥EC,∴∠OAF=∠OCE.
在△AOF和△COE中,
∵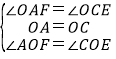
∴△AOF≌△COE,∴OF=OE.又∵AO=OC,
∴四边形AECF是平行四边形.
(2)四边形AECF是菱形.
理由如下:∵∠DAB=∠BCD=90°,点E为BD的中点,
∴AE=![]() BD,CE=
BD,CE=![]() BD,∴AE=CE.
BD,∴AE=CE.
由(1)知四边形AECF是平行四边形,
∴四边形AECF是菱形.

【题目】2017年12月,旗团委号召各校组织开展捐赠衣物的“暖冬行动”![]() 某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:
某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:
班级 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
人数 | 40 | 43 | 45 | 44 | 40 | 38 |
件数 |
|
|
|
|
|
|
![]() 捐赠衣物最多的班比最少的班多多少件?
捐赠衣物最多的班比最少的班多多少件?
![]() 该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?
该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?
【题目】小洋八年级下学期的数学成绩(单位:分)如下表所示:
测试 类别 | 平时 | 期中 考试 | 期末 考试 | |||
测验1 | 测验2 | 测验3 | 测验4 | |||
成绩 | 106 | 102 | 115 | 109 | 112 | 110 |
(1)计算小洋该学期的数学平时平均成绩;
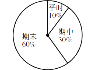
(2)如果该学期的总评成绩是根据如图所示的权重计算的,请计算出小洋该学期的数学总评成绩.