题目内容
【题目】如图，在△ABC中，CA=CB，∠ACB=90°，AB=2，点D为AB的中点，以点D为圆心作圆心角为90°的扇形DEF，点C恰在弧EF上，则图中阴影部分的面积为 ．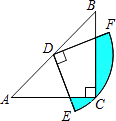 
【答案】
﹣ 
【解析】解：连接CD，作DM⊥BC，DN⊥AC．
∵CA=CB，∠ACB=90°，点D为AB的中点，
∴DC= 
AB=1，四边形DMCN是正方形，DM= 
．
则扇形FDE的面积是： 
= 
．
∵CA=CB，∠ACB=90°，点D为AB的中点，
∴CD平分∠BCA，
又∵DM⊥BC，DN⊥AC，
∴DM=DN，
∵∠GDH=∠MDN=90°，
∴∠GDM=∠HDN，
在△DMG和△DNH中，
，
∴△DMG≌△DNH（AAS），
∴S四边形DGCH=S四边形DMCN= ．
则阴影部分的面积是： ﹣ ．
故答案为 ﹣ ．
连接CD，作DM⊥BC，DN⊥AC，证明△DMG≌△DNH，则S四边形DGCH=S四边形DMCN，求得扇形FDE的面积，则阴影部分的面积即可求得．
练习册系列答案
相关题目
【题目】为了解今年初四学生的数学学习情况，某校在第一轮模拟测试后，对初四全体同学的数学成绩作了统计分析，绘制如下图表：请结合图表所给出的信息解答系列问题：
成绩 | 频数 | 频率 |
优秀 | 45 | b |
良好 | a | 0.3 |
合格 | 105 | 0.35 |
不合格 | 60 | c |
（1）该校初四学生共有多少人？
（2）求表中a，b，c的值，并补全条形统计图．
（3）初四（一）班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍，求恰好选中甲、乙两位同学的概率．
