Question

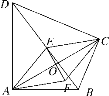
【题目】将两张完全相同的矩形纸片ABCD、FBED按如图方式放置，BD为重合的对角线．重叠部分为四边形DHBG，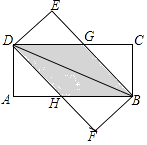

（1）试判断四边形DHBG为何种特殊的四边形，并说明理由；
（2）若AB=8，AD=4，求四边形DHBG的面积．

Answer 1

【答案】
（1）解：四边形DHBG是菱形．理由如下：

∵四边形ABCD、FBED是完全相同的矩形，

∴∠A=∠E=90°，AD=ED，AB=EB．

在△DAB和△DEB中， ，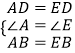

∴△DAB≌△DEB（SAS），

∴∠ABD=∠EBD．

∵AB∥CD，DF∥BE，

∴四边形DHBG是平行四边形，∠HDB=∠EBD，

∴∠HDB=∠HBD，

∴DH=BH，

∴DHBG是菱形．

（2）解：由（1），设DH=BH=x，则AH=8﹣x，

在Rt△ADH中，AD2+AH2=DH2，即42+（8﹣x）2=x2，

解得：x=5，即BH=5，

∴菱形DHBG的面积为HBAD=5×4=20．

【解析】（1）四边形DHBG是菱形．理由如下：根据矩形的性质得出∠A=∠E=90°，AD=ED，AB=EB．进而利用SAS判断出△DAB≌△DEB，再根据全等三角形的性质得出∠ABD=∠EBD，然后判断出四边形DHBG是平行四边形，∠HDB=∠EBD，然后根据平行四边形的性质得出∠HDB=∠HBD，从而知道DH=BH，进而得出结论；
（2）由（1），设DH=BH=x，则AH=8﹣x，在Rt△ADH中，由勾股定理得出关于x的方程，求解即可，然后根据菱形面积公式算出面积。
【考点精析】掌握勾股定理的概念和平行四边形的判定与性质是解答本题的根本，需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积．