题目内容
【题目】如图,网格中有格点△ABC与△DEF.

(1)△ABC与△DEF是否全等?(不说理由.)
(2)△ABC与△DEF是否成轴对称?(不说理由.)
(3)若△ABC与△DEF成轴对称,请画出它的对称轴l.并在直线l上画出点P,使PA+PC最小.
【答案】(1)△ABC△DEF;(2)△ABC与△DEF成轴对称;(3)见详解
【解析】
(1)根据坐标系可以看出△ABC与△DEF三边相等,即可证明△ABC与△DEF全等;(2)根据坐标系可以看出△ABC与△DEF关于某条直线对称;(3)利用网格特点,作AD的垂直平分线即可得出对称轴l,连接CD,与直线l的交点即为所求;
解:(1)根据坐标系可以看出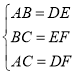
∴△ABC△DEF;
(2)根据坐标系可以看出△ABC与△DEF关于直线l成轴对称;
(3)要使PA+PC最小则A,P,C三点共线的时候即为所求因为点D为A的对称点,所以连接PD与对称轴交点即为所求,如图所示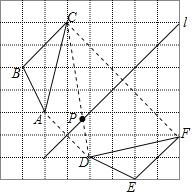
点P即为所求.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目