题目内容
【题目】如图，在△ABC中，AB=AC=m，P为BC上任意一点，则PA2+PBPC的值为（ ）
A. m2 B. m2+1 C. 2m2 D. （m+1）2
【答案】A
【解析】
如图，作AD⊥BC交BC于D，根据勾股定理得AB2=BD2+AD2，AP2=PD2+AD2，再根据D是BC的中点，整理得到AB2﹣AP2=PBPC，再把AB=m代入求解即可.
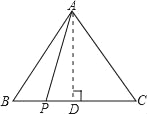解：如图，作AD⊥BC交BC于D，
AB2=BD2+AD2 ①，
AP2=PD2+AD2 ②，
①﹣②得：
AB2﹣AP2=BD2﹣PD2，
∴AB2﹣AP2=（BD+PD）（BD﹣PD），
∵AB=AC，
∴D是BC中点，
∴BD+PD=PC，BD﹣PD=PB，
∴AB2﹣AP2=PBPC，
∴PA2+PBPC=AB2=m2．
故选A.
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
