题目内容
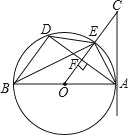
【题目】如图,AB是⊙O的直径,AC切⊙O于点A,AD是⊙O的弦,OC⊥AD于F交⊙O于E,连接DE,BE,BD,AE.
(1)求证:∠C=∠BED;
(2)如果AB=10,tan∠BAD=![]() ,求AC的长;
,求AC的长;
(3)如果DE∥AB,AB=10,求四边形AEDB的面积.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据切线性质、垂直的性质、直角三角形的两个锐角互余的性质求得∠C+∠AOC=∠AOC+∠BAD=90°,即∠C=∠BAD;然后由圆周角定理推知∠BED=∠BAD;最后由等量代换证得∠C=∠BED;
(2)根据锐角三角函数的定义求AC的长;
(3)根据已知条件推知AE=BD=DE,然后由圆的弧、弦、圆心角间的关系知![]() ,从而求得∠BAD=30°;然后由直径AB所对的圆周角∠ADB=90°可以求得直角三角形ABD中30°所对的直角边是斜边的一半BD
,从而求得∠BAD=30°;然后由直径AB所对的圆周角∠ADB=90°可以求得直角三角形ABD中30°所对的直角边是斜边的一半BD![]() AB=5,DE=5;最后(过点D作DH⊥AB于H)在直角三角形HDA中求得高线DH的长度,从而求得梯形ABDE的面积.
AB=5,DE=5;最后(过点D作DH⊥AB于H)在直角三角形HDA中求得高线DH的长度,从而求得梯形ABDE的面积.
(1)∵AB是⊙O的直径,CA切⊙O于A,∴∠C+∠AOC=90°;
又∵OC⊥AD,∴∠OFA=90°,∴∠AOC+∠BAD=90°,∴∠C=∠BAD.
又∵∠BED=∠BAD,∴∠C=∠BED.
(2)由(1)知∠C=∠BAD,tan∠BAD![]() ,∴tan∠C
,∴tan∠C![]() .
.
在Rt△OAC中,tan∠C![]() ,且OA
,且OA![]() AB=5,∴
AB=5,∴![]() ,解得:
,解得:![]() .
.
(3)∵OC⊥AD,∴![]() ,∴AE=ED.
,∴AE=ED.
又∵DE∥AB,∴∠BAD=∠EDA,∴![]() ,∴AE=BD,∴AE=BD=DE,∴
,∴AE=BD,∴AE=BD=DE,∴![]() ,∴∠BAD=30°.
,∴∠BAD=30°.
又∵AB是直径,∴∠ADB=90°,∴BD![]() AB=5,DE=5.在Rt△ABD中,由勾股定理得:AD
AB=5,DE=5.在Rt△ABD中,由勾股定理得:AD![]() ,过点D作DH⊥AB于H.
,过点D作DH⊥AB于H.
∵∠HAD=30°,∴DH![]() AD
AD![]() ,∴四边形AEDB的面积
,∴四边形AEDB的面积![]() .
.

【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示.
x | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -12 | -2 | 4 | 6 | 4 | … |
给出下列说法:①抛物线与y轴的交点为(0,6);②抛物线的对称轴是在y轴的右侧;③抛物线一定经过点(3,0);④当x<0时,函数值y随x的增大而减小.
从表中可知,上述说法正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个