题目内容
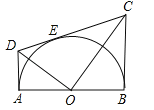
【题目】如图，在平面直角坐标系中，直线
经过第一、二、四象限，点
在上．
（1）在图中标出点
；
（2）若
，且过点
，求直线的解析式；
（3）在（2）的条件下，直接写出当
时，
的取值范围．
【答案】（1）见解析；（2）直线l的表达式为：y=﹣
x+2；（3）
【解析】
（1）根据
在y轴上，又在
上，即可找出A点；
（2）利用待定系数法求出直线l的表达式即可；
（3）求出直线l与x轴的交点坐标，根据图像进行判断即可.
解：（1）如图所示，A点为所求.
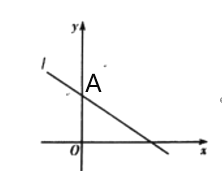
（2）设直线l的表达式为：y=kx+b，
把（0，2），（﹣3，4）分别代入y=kx+b得：
，
解得：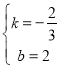
，
故直线l的表达式为：y=﹣x+2；
（3）当y=0时，0=
x+2，
解得：x=3，
所以直线l与x轴交于（3，0），
∴当
时，
的取值范围为：.
练习册系列答案
名师点拨卷系列答案
相关题目
【题目】某家具商场计划购进某种餐桌、餐椅进行销售，有关信息如下表：
原进价（元/张） | 零售价（元/张） | 成套售价（元/套） | |
餐桌 | a | 270 | 500 |
餐椅 | b | 70 |
若购进3张餐桌18张餐椅需要1170元；若购进5张餐桌25张餐椅需要1750元．
（1）求表中a，b的值；
（2）若该商场购进餐椅的数量是餐桌数量的5倍还多20张，且餐桌和餐椅的总数量不超过200张．该商场计划将全部餐桌配套销售（一张餐桌和四张餐椅配成一套），其余餐椅以零售方式销售．设购进餐桌的数量为x（张），总利润为W（元），求W关于x的函数关系式，并求出总利润最大时的进货方案．
