题目内容
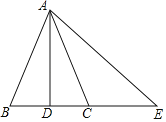
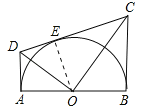
【题目】如图，AB为半圆O的在直径，AD、BC分别切⊙O于A、B两点，CD切⊙O于点E，连接OD、OC，下列结论：①∠DOC=90°，②AD+BC=CD，③
，④OD：OC=DE：EC，⑤
，正确的有（ ）
A. 2个 B. 3个 C. 4个 D. 5个
【答案】D
【解析】
试题连接OE，如图所示：∵AD与圆O相切，DC与圆O相切，BC与圆O相切，∴∠DAO=∠DEO=∠OBC=90°，∴DA=DE，CE=CB，AD∥BC，∴CD=DE+EC=AD+BC，选项②正确；
在Rt△ADO和Rt△EDO中，∵OD=OD，DA=DE，∴Rt△ADO≌Rt△EDO（HL），∴∠AOD=∠EOD，同理Rt△CEO≌Rt△CBO，∴∠EOC=∠BOC，又∠AOD+∠DOE+∠EOC+∠COB=180°，∴2（∠DOE+∠EOC）=180°，即∠DOC=90°，选项①正确；
∴∠DOC=∠DEO=90°，又∠EDO=∠ODC，∴△EDO∽△ODC，∴
，即
，选项⑤正确；
∵∠AOD+∠COB=∠AOD+∠ADO=90°，∠A=∠B=90°，∴△AOD∽△BOC，∴
，选项③正确；
同理△ODE∽△OEC，∴
，选项④正确；
故选D．
练习册系列答案
相关题目
