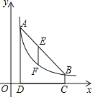
题目内容
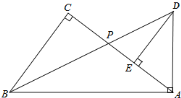
【题目】如图,![]() ,
,![]() 均为等边三角形,点
均为等边三角形,点![]() ,
,![]() ,
,![]() 在同一条直线上,连接
在同一条直线上,连接![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,下列结论正确的有_________.
,下列结论正确的有_________.
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 平分
平分![]()
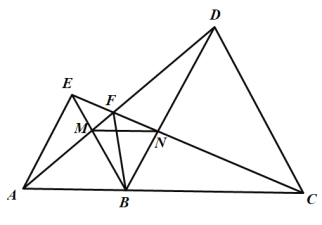
【答案】①②③⑤.
【解析】
由题意根据全等三角形的判定和性质以及等边三角形的性质和角平分线的性质,对题干结论依次进行分析即可.
解:∵△ABE,△BCD均为等边三角形,
∴AB=BE,BC=BD,∠ABE=∠CBD=60°,
∴∠ABD=∠EBC,
在△ABD和△EBC中,
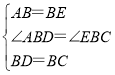
∴△ABD≌△EBC(SAS),
∴AD=EC,故①正确;
∴∠DAB=∠BEC,
又由上可知∠ABE=∠CBD=60°,
∴∠EBD=60°,
在△ABM和△EBN中,
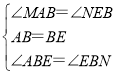
∴△ABM≌△EBN(ASA),
∴BM=BN,故②正确;
∴△BMN为等边三角形,
∴∠NMB=∠ABM=60°,
∴MN∥AC,故③正确;
若EM=MB,则AM平分∠EAB,
则∠DAB=30°,而由条件无法得出这一条件,
故④不正确;
如图作![]()
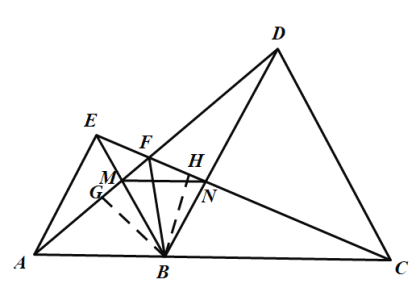
∵由上可知△ABD≌△EBC,
∴两个三角形对应边的高相等即![]() ,
,
∴![]() 是
是![]() 的角平分线,即有
的角平分线,即有![]() 平分
平分![]() ,故⑤正确.
,故⑤正确.
综上可知:①②③⑤正确.
故答案为:①②③⑤.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目