题目内容
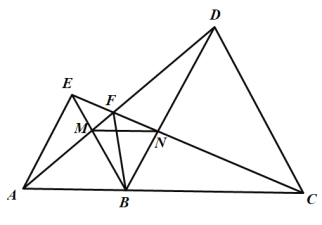
【题目】已知，正方形ABPD的边长为3，将边DP绕点P顺时针旋转90°至PC，E、F分别为线段DP、CP上两个动点（不与D、P、C重合），且DE=CF，连接BE并延长分别交DF、DC于H、G．
（1）①求证：△BPE≌△DPF，②判断BG与DF位置关系并说明理由；
（2）当PE的长度为多少时，四边形DEFG为菱形并说明理由；
（3）连接AH，在点E、F运动的过程中，∠AHB的大小是否发生改变？若改变，请说出是如何变化的；若不改变，请求出∠AHB的度数．
【答案】（1）①见解析，②BG⊥DF；（2）当PE=3
﹣3时，四边形DEFG为菱形；
（3）45°．
【解析】分析：
（1）①由已知条件易得BP=DP=PC，∠BPE=∠DPF=90°结合DE=CF可得PE=PF，由此即可得到△BPE≌△DPF；②由△BPE≌△DPF可得∠EBP=∠FDP，结合∠FDP+∠BFH=90°，可得∠EBP+∠BFH=90°，从而可得∠BHP=90°，由此可得BG⊥DF；
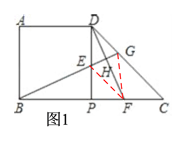
（2）如下图1，连接EF、GF，由题意可知，要使四边形DEFG是菱形，则必须使DE=EF，由（1）中所得△BPE≌△DPF可得PF=PE，设PE=x，则DE=3-x=EF，由此在Rt△PEF中由勾股定理建立方程，解方程即可求得此时PE=x=
，解题时把PE=作为一个条件，结合题目中的其它条件去证明此时四边形DEFG为菱形即可；
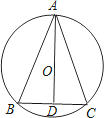
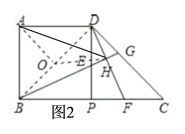
（3）如图2，连接BD，作出BD的中点O，连接AO，HO，由已知条件结合（1）中所得BG⊥DF易得OA=OB=OD=OH=
BD，由此可得点A、B、H、D在以O为圆心、OA为半径的圆上，从而可得∠AHB=∠ADB=45°．
详解：
（1）①证明：由旋转的性质可知，△DPC是等腰直角三角形，
∵四边形ABPD是正方形，
∴BP=PD=PC，∠BPE=∠DPF=90°，
∵DE=CF，
∴PE=PF，
在△BPE和△DPF中，
BP=PD，∠BPE=∠DPF，PE=PF，
∴△BPE≌△DPF；
②∵△BPE≌△DPF，
∴∠EBP=∠FDP，又∠FDP+∠BFH=90°，
∴∠EBP+∠BFH=90°，
∴∠BHP=90°，
∴BG⊥DF；
（2）当PE=时，四边形DEFG为菱形；理由如下：
在正方形ABPD中，BP=PD=3，
∵PE=，EF=PE，
∴EF=
=6﹣3，DE=PD-PE=6﹣3，
∴EF=ED，
∵BG⊥DF，
∴EG垂直平分DF，
∴GD=GF，
∵∠PEF=∠PDC=45°，
∴EF∥DG，
∴∠EFD=∠FDG，
∵DE=EF，
∴∠EFD=∠EDF，
∴∠EDG=∠FDE，
∵BG⊥DF，
∴∠DEG=∠DGE，
∴DE=DG，
∴DE=DG=GF=EF，
∴四边形DEFG是菱形；
（3）∠AHB的大小不变，∠AHB=45°，
连接BD，取BD的中点O，连接OA、OH，
∵四边形ABCD是正方形，
∴∠BAD=90°，∠ADB=45°，
∵BG⊥DF，
∴∠DHB=90°，
则OA=OB=OD=OH=BD，
∴点A、B、H、D在以O为圆心、OA为半径的圆上，
∴∠AHB=∠ADB=45°．
