Question

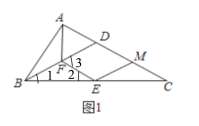
【题目】在直角三角形ABC中，∠BAC=90°，（AC＞AB），在边AC上取一点D，使得BD=CD，点E、F分别是线段BC、BD的中点，连接AF和EF，作∠FEM=∠FDC，交AC于点M，如图1所示.

（1）请判断四边形EFDM是什么特殊的四边形，并证明你的结论；

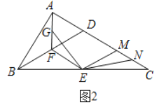
（2）将∠FEM绕点E顺时针旋转到∠GEN，交线段AF于点G，交AC于点N，如图2所示，请证明：EG=EN；

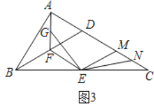
（3）在第（2）条件下，若点G是AF中点，且∠C=30°，AB=3，如图3，求GE的长度.

Answer 1

【答案】（1）菱形，理由见解析；（2）见解析；（3）

【解析】

（1）先判断出DF∥EM，进而判断出EF∥CD，得出四边形DFEM是平行四边形，再判断出DF=DM，即可得出结论；
（2）先判断出∠FEG=∠MEN，进而判断出∠DAF=∠ADF，即可得出∠AFE=∠CDF，进而得出∠AFE=∠CME，进而判断出△EFG≌△EMN（AAS），即可得出结论；

（3）先求出BC=4，进而求出CE=2，BD=，CD=，进而求出FG=AF=,即可求出MN=FG=，再求出EF=CD=，进而得出CN=，即可求出EH=CN=，CH=EH=，进而得出EH=CE-CH=，最后用勾股定理即可得出结论．

菱形，理由如下：

∵E，F分别是BC，CD中点.

∴FB＝FD，，

∴，

又，

∴，

∴∴,M为DC中点.

又DB＝DC，

，

∴，

∴菱形FEMD，

（2）如图，

由旋转知，∠FEM=∠GEN，

∴∠FEG=∠MEN，

在Rt△ABD中，点F是BD中点，

∴AF=DF，

∴∠DAF=∠ADF，

∵EF∥CD，

∴∠ADF=∠DFE，

∴∠DAF=∠DFE，

∴∠AFE=∠AFD+∠EFD=∠AFD+∠ADF=∠CDF，

∵EM∥BD，

∴∠CDF=∠EMN，

∴∠AFE=∠CME，

由（1）知，四边形DFEM是菱形，

∴EF=EM，

∴△EFG≌△EMN（AAS），

∴EG=EN；

（3）如图，

在Rt△ABC中，∠C=30°，AB=2，

∴BC=4，∠ABC=60°，

∵点E是BC的中点，

∴CE=2，

∵BD=CD，

∴∠CBD=∠C=30°，

∴∠ABD=30°，

∴BD=，

∴CD=，AF=BD=，

∵G是AF的中点，

∴FG=AF=，

∵△EFG≌△EMN（AAS），

∴EG=EN，MN=FG=，

∵E，F是BC，BD的中点，

∴EF=CD=，

∴DM=EF=，

∴CN=CD-DM-MN=

过点N作NH⊥BC于H

∴EH=CN=，CH=EH=，

∴EH=CE-CH=，

在Rt△ENH中，EN=，

∴EG=．