Question

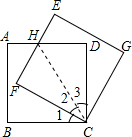
如图，边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到的正方形EFCG，EF交AD交于点H．
（1）求证：DH=FH．
（2）求DH的长．

Answer 1

（1）证明：连接HC．
∵正方形EFCG是由正方形ABCD绕点C旋转后得到的，
∴CD=CF，∠D=∠F=Rt∠．
在Rt△CDH和Rt△CFH中，

HC=HC CD=CF

，
∴Rt△CDH≌Rt△CFH（HL），
∴DH=FH；

（2）∵正方形EFCG是由正方形ABCD绕点C旋转30°后得到的，
∴∠1=30°，∠BCD=∠1+∠2+∠3=90°．
由（1）得Rt△CDH≌Rt△CFH．
∴∠2=∠3=

1

2

（90°-∠1）=30°
∵在Rt△CDH中，∠3=30°，
∴DH=

1

2

HC，即HC=2DH．
由勾股定理得，HC²=DH²+CD²，
∵CD=3，
∴（2DH）²=DH²+3²，
解得，DH=

3

．